De investigación.

Propuesto por Juan Bosco Romero Márquez, profesor colaborador de la Universidad de Valladolid.

Problema 421.- Sea ABC un triángulo rectángulo en A, c<b <a. Trazamos la recta que
pasa por el incentro I, y el circuncentro O, que corta a la prolongación de AC, en  D y AB en E, respectivamente.

  Probar si es cierto o no:

  a) Que AD= a/2 si sólo si B =60

  b) Si F= AO∩EC , entonces IF // AB si y sólo si B=60.

Romero, J.B. (2007): Comunicación personal.

Solución de del primer apartado de Saturnino Campo Ruiz, profesor del IES Fray Luis de León, de Salamanca.

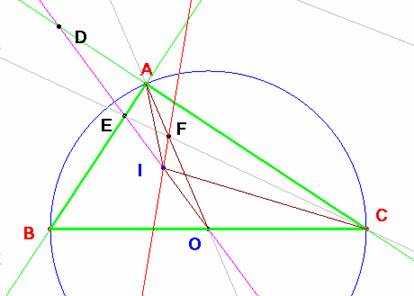
Sean b y g los ángulos agudos de vértices B y C respectivamente.

a) Si el ángulo B mide 60º, el triángulo ABO es equilátero, por tanto la bisectriz de B es también mediatriz del triángulo AIO. Este triángulo es pues, isósceles. Tenemos <BAI=45º y <BAO =60º por tanto <IAO=<IOA=15º. En el triángulo DAO, este ángulo mide 90+60=150º. Si <IOA=15º ha de ser también de 15º el otro ángulo ADO. Y con esto queda probado que DA =AO.

Recíprocamente, si el triángulo ADO es isósceles, el ángulo IOA mide d = g/2 =ICA.

Calculemos la longitud del segmento AI en los triángulos AIO y AIC respectivamente utilizando el teorema de los senos:

En AIO con A=45-g, O=d y I=135+d se tiene:.

En AIC donde A=45, C=d y I=135-d: .

Igualando los segundos miembros queda: =.

Si elevamos al cuadrado resulta:

.

Sustituyendo sen g = c/a queda

.

Si ahora ponemos b² = a²- c² y multiplicamos por a+c queda, .

Desarrollando esta última obtenemos a = 2c, que implica que el ángulo b=60º.