Problema 421.- (Propuesto por J. Bosco Romero Márquez, profesor colaborador de la Universidad de Valladolid).

Sea ABC un triángulo rectángulo en A, . Trazamos la recta que pasa por el incentro I y el circuncentro O, que corta a la prolongación de AC en D y AB en E, respectivamente.

Probar si es cierto o no:

(a) que si y sólo si

(b) si , entonces IF//AB si y sólo si

Romero, J.B. (2007): Comunicación personal

Resolución: (Vicente Vicario García, I.E.S. “El Sur”, Huelva)

(a) Por ser rectángulo el triángulo ABC dado, su circuncentro corresponde al punto medio de su hipotenusa. Denotaremos inicialmente el punto S como el punto de corte de la perpendicular al lado AC trazada desde el circuncentro O y la recta paralela al lado AC que contiene el punto E. Sea N el punto de corte de la recta OS con el lado AC. Por ser AC>AB el punto de corte D necesariamente pertenece a la prolongación del lado AC. Necesitamos un lema que demostramos a continuación:

Lema: “Con la notación habitual en el triángulo ABC rectángulo en A, se tiene que el radio de su circunferencia inscrita r viene dado por ”.

Demostración: Basta observar que a partir del área del triángulo y el teorema de Pitágoras, tenemos que

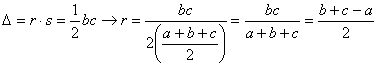
Demostremos ahora la condición necesaria

(a1) si .

Demostración: A partir de la semejanza de los triángulos OIS y ODN tenemos

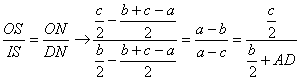
ahora, si suponemos que entonces se tiene que

y, por tanto,

Demostremos la condición suficiente

(a2) si

Demostración: Puesto que , entonces y . En consecuencia, a partir de la relación de semejanza anterior tenemos que

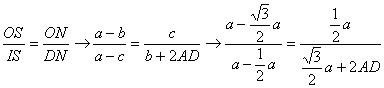
de donde se deduce fácilmente que.

Demostremos el contenido del apartado (b). Para ello, emplearemos la geometría de coordenadas siendo , , . Demostremos la condición necesaria

(b1) si IF//AB

Demostración: Si IF//AB esto quiere decir que, por hipótesis, la abscisa del punto F es precisamente la misma que la del incentro I, es decir, . Las coordenadas del punto F son las soluciones del siguiente sistema de ecuaciones lineales formado por las rectas AO y CE

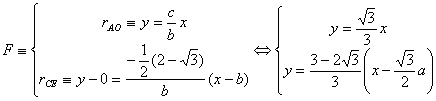
Entonces, el apartado estará demostrado si probamos que igualando la abscisa de la solución del sistema anterior al radio de la circunferencia inscrita, se deduce que el ángulo B es de 60º.

La solución x del sistema anterior es tal que y es fácil verificar ahora que con , se cumple la igualdad para , sustituyendo y .

Demostremos ahora la condición suficiente (b2)

(b2) si

Demostración: Puesto que , entonces y también . Por tanto, el radio de la circunferencia inscrita al triángulo ABC será

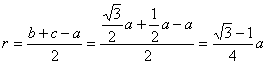
Por otra parte, las coordenadas del punto F serán las soluciones del sistema

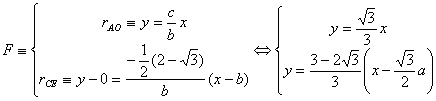
y el apartado (b2) estará demostrado, si probamos que la abscisa del punto F que resulta como solución del sistema de ecuaciones lineales anterior, coincide con el valor del radio de la circunferencia inscrita anteriormente expresado. Así, se tendría que IF//AB.

Pero esto es fácil de ver, puesto que la abscisa de la solución del sistema anterior viene dada por

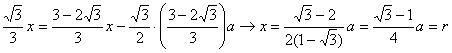
donde la última igualdad es evidente a partir de una simple racionalización.