Solución del
Problema 422
ABC es cuyas tres bisectrices se cortan en P. P se proyecta respectivamente en H y K en los segmentos AB y AC. ¿Cómo es el ángulo formado por las rectas AP y HK?
Solución de Alejandro Cipriano Coronel,estudiante de ingeniería de
De acuerdo a los datos el diseño del problema sería como sigue:
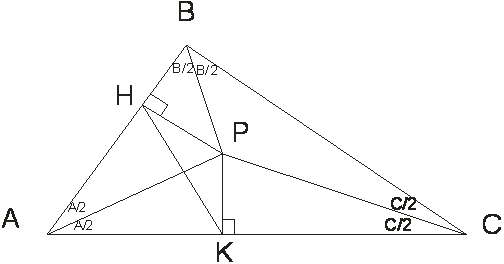
Además se cumple que: A+B+C = 180º; Entonces A/2 + B/2 + C/2 = 90º.
A la intersección de HK y AP llamémosle R.
Por el teorema de la bisectriz se tiene que HP = PK y AH = AK; entonces:
· m< PHK = m< PKH
·
m<
APH = m< APK = (B/2 + C/2).
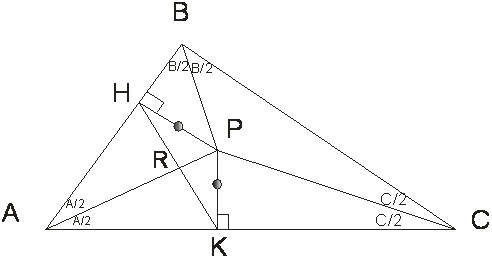
· Además m< PHK = m< PKH = A/2
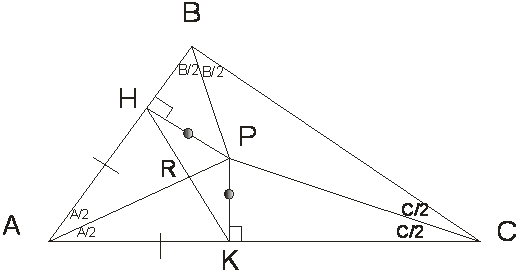
Finalmente
en el triángulo RPK o HRP se cumple: m <R + m< RPK + m< RKP = 180º
Entonces:
m <R = 180º - (m <RPK + m <RKP)
m<R = 180º - [(B/2 + C/2) +
A/2] = 180º - 90º = 90º
Por lo
tanto: m< R = 90º …. Rpta.
UN MÉTODO MÁS RÁPIDO

Como el
triángulo AHK es isósceles (AH = AK); Entonces
m< AHK =
m< AKH = 90º - A/2
Además en el triángulo ARK se cumple A/2 + m< AKR + m< R = 180º
m<R
= 180º - A/2 –m<AKR = 180º - A/2 – (90º - A/2) =
90º
Por lo
tanto: m<R = 90º … Rpta.