Para el aula
Problema 422
ABC es un triángulo cuyas tres bisectrices se cortan en P. P se proyecta respectivamente en H y K en los segmentos AB y AC. ¿Cómo es el ángulo formado por las rectas AP y HK?
Tu turno:
Resuelto por JULIÁN SANTAMARÍA TOBAR profesor de Dibujo del IES
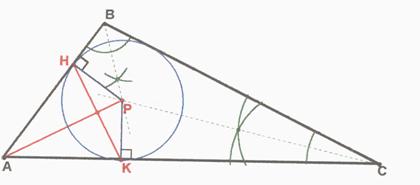
El triángulo HPK es isósceles porque PH y PK son radios de la circunferencia
inscrita. El triángulo HAK también es isósceles porque AH y AK son los
segmentos tangentes del punto A a la circunferencia
inscrita. Ambos triángulos forman el cuadrilátero bi-isósceles
AKPH. La diagonal AP es el eje de simetría del cuadrilátero por ser el eje de
de simetría de ambos triángulos. Por lo tanto si el simétrico de H con respecto
a la diagonal AP resulta K el ángulo de las diagonales HK y AP es de 90º