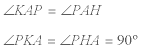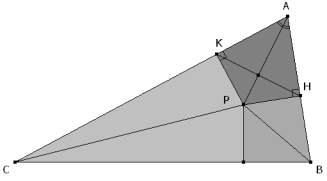
Para el aula.

Problema 422 .

pABC es un triángulo cuyas tres bisectrices se cortan en P. P se proyecta respectivamente en H y K en los segmentos AB y AC. ¿Cómo es el ángulo formado por las rectas AP y HK?

Tu turno:

Berrondo-Agrell, M. (2006) 101 enigmas de geometría, juegos divertidos para potenciar tu mente. Ediciones Ceac Barcelona.(p.64)

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (17 noviembre de 2007)

DIBUJAMOS EL ENUNCIADO

figura 1

RAZONAMIENTO 1

Los triángulos AKP  y AHP  tienen dos ángulos iguales

y un lado común AP;   por lo tanto dichos triángulos son congruentes y simétricos respecto el lado común; luego K  y H  son simétricos y por lo tanto

KH  es perpendicular a AP  y el ángulo formado es de 90º.

RAZONAMIENTO 2

AP  es la bisectriz del ángulo A;  por lo tanto el punto P  equidista de AB  y AC  y ello implica que

lo que significa que el triángulo AKH  es isósceles y por lo tanto la bisectriz AP  del ángulo A  es perpendicular⁽¹⁾ a la base KH,  luego

KH  es perpendicular a AP  y el ángulo formado es de 90º.

⁽¹⁾Esto, en sí mismo, ya es un bonito teorema a demostrar.