Problema 423

Sea  ABC un triángulo rectángulo en A, de hipotenusa a, y de altura correspondiente, h. Probar  que :

.

Solución Ricard Peiró:

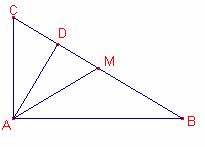
Sea la mediana sobre la hipotenusa.

La mediana sobre la hipotenusa d’un triángulo rectángulo mide la mitad de la hipotenusa, .

, la igualdad se alcanza cuando el triángulo rectángulo es isósceles.

Entonces, .

a)

.

Pero .

La desigualdad es estricta, por tanto,

b)

Consideremos la función: .

Es una parábola cóncava, la función es definida negativa y creciente en ,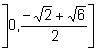

Entonces, La función es creciente en . Por tanto, .

Por tanto, .