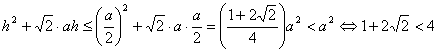Problema 423. Sea un triángulo ABC rectángulo en A, de hipotenusa a y de altura relativa correspondiente h. Probar que

                                  

Resolución: (Vicente Vicario García, I.E.S. El Sur, Huelva)

            Demostraremos que las desigualdades anteriores, en realidad, son estrictas. Necesitamos un lema que demostramos a continuación:

Lema: “El valor máximo que toma la altura relativa a la hipotenusa en un triángulo rectángulo de hipotenusa fija a, es  ”.

Demostración: basta observar el arco capaz correspondiente a la semicircunferencia de diámetro a y comprobar que la altura máxima corresponde a la mitad de la hipotenusa.

            Demostremos ahora las desigualdades. Para la primera desigualdad tenemos que

                       

pero , según el lema , con lo que la desigualdad queda demostrada si se cumple

                       

con lo que la desigualdad se cumple y además es estricta.

            Para demostrar la segunda desigualdad tenemos

                       

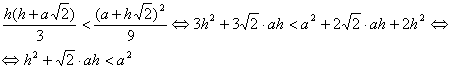
Pero esta última desigualdad es cierta y además estricta, ya que, de nuevo, aplicando el lema anterior