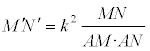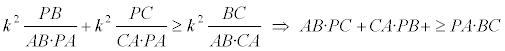De investigación Propuesto por José María Pedret. Ingeniero Naval. (Esplugas de Llobregat, Barcelona) Problema 424 TEOREMA DE POMPEÏU Descubierto por el matemático rumano DIMITRIE POMPEÏU, el teorema es bastante simple; y dice así
A partir de aquí, al triángulo de lados iguales a las longitudes PA, PB, PC lo denominaremos triángulo de Pompeïu. Este teorema ya fue abordado en el problema nº 77 del Laboratorio virtual de triángulos con Cabri II. József Sándor, en (On the Geometry of Equilateral Triangles, Forum Geometricorum Volume 5 (2005)), presenta una indicación para la demostración del teorema por medio del teorema de Ptolomeo, una determinación gráfica del triángulo de Pompeïu y deriva de ella un cálculo del área. Nuestra propuesta, orientada a Cabri® II Plus es la siguiente:
Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (noviembre de 2007) |
|
INTRODUCCIÓN |
|
Abordamos la resolución del enunciado presentando, en primer lugar, dos proposiciones previas que necesitaremos para completar la demostración de los resultados pedidos. A continuación desarrollamos la demostración del teorema distinguiendo tres casos; que el punto P sea interior al triángulo equilátero ABC, que el punto P esté sobre el círculo circunscrito o que el punto P sea exterior al triángulo equilátero ABC. Acabamos con un apéndice donde se desarrollan las indicaciones de József Sándor para otra demostración del teorema de Pompeïu, construcción y determinación del área del triángulo de Pompeïu. La construcción, que indica József Sándor, sólo es válida cuando P es interior al triángulo equilátero ABC. |
|
PROPOSICIONES PREVIAS |
|
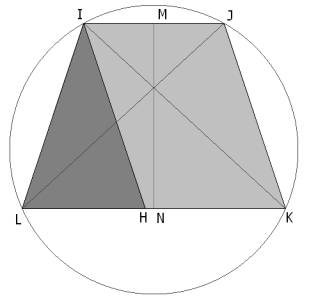
PROPOSICIÓN 1
Por definición de trapecio isósceles, JK=IL. Por I una paralela a JK que corta a KL en H entonces el triángulo LIH es isósceles ya que IL=JK=IH; entonces se cumple la igualdad de los ángulos de la base del triángulo
Pero si trazamos una perpendicular a las bases, que las corta respectivamente en M y N, formamos el cuadrilátero IMNL y como los ángulos de un cuadrilátero suman 360°
y si aplicamos la igualdad anterior
por lo tanto los ángulos opuestos son suplementarios y por tanto el trapecio isósceles es inscriptible. PROPOSICIÓN 2
Observando los arcos en el círculo circunscrito al trapecio tenemos
y como la igualdad de arcos conlleva la igualdad de cuerdas
en consecuencia las diagonales de un trapecio isósceles son iguales. |
|
SOLUCION |
|
DIBUJO DEL ENUNCIADO
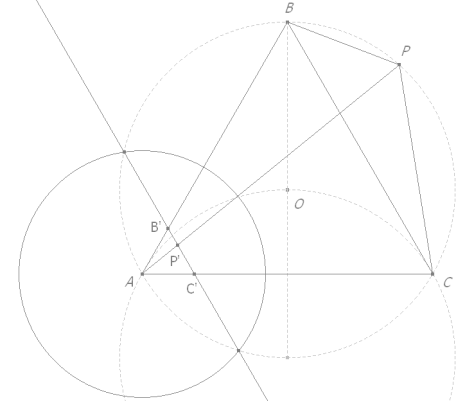
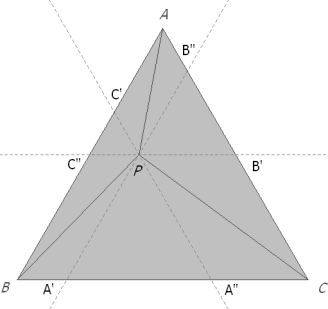
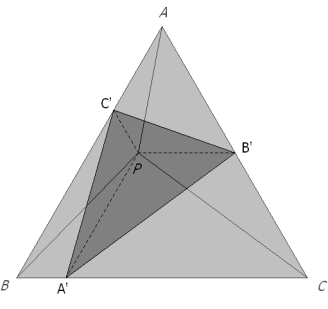
Dibujamos un triángulo equilátero ABC y un punto cualquiera P en su interior.
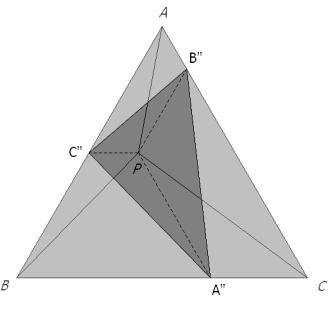
Trazamos por P rectas paralelas a los lados del triángulo. La paralela a AB corta a BC en A’. La paralela a BC corta a CA en B’. La paralela a CA corta a AB en C’. La paralela a AB corta a CA en B”. La paralela a BC corta a AB en C”. La paralela a CA corta a BC en A”. |
|
SI P ES UN PUNTO INTERIOR AL TRIÁNGULO EQUILÁTERO ABC
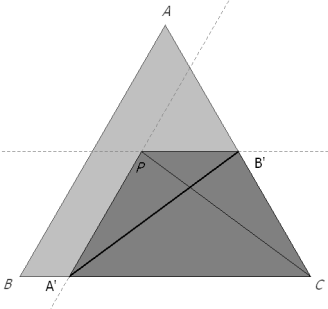
Observamos que el polígono PA’CB’ es un trapecio isósceles, de donde aplicando la proposición 2
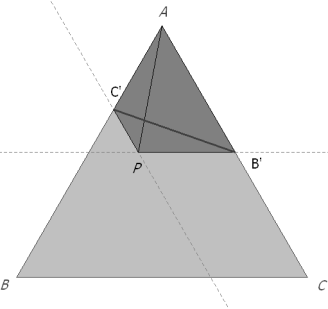
El otro polígono PB’AC’ también es isósceles y por tanto, de la igualdad de diagonales
Análogo a los dos casos interiores, la igualdad de diagonales en PC’BA’ da
Reunimos los tres resultados anteriores y obtenemos el triángulo A’B’C’, triángulo de Pompeïu inscrito en el triángulo equilátero ABC ya que
La condición equilátera de ABC asegura que los tres trapecios que aparecen en la construcción son isósceles.
Podríamos hacer el mismo razonamiento sobre los trapecios isósceles PC”BA”, PA”CB”, PB”AC” y A”B”C” sería un segundo triángulo de Pompeïu inscrito en el triángulo equilátero ABC ya que
|
|
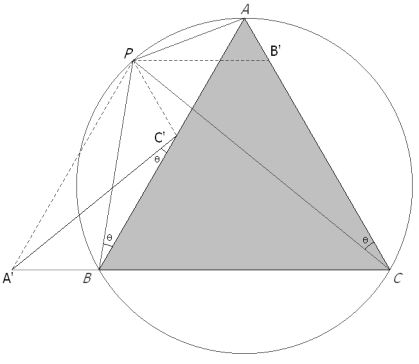
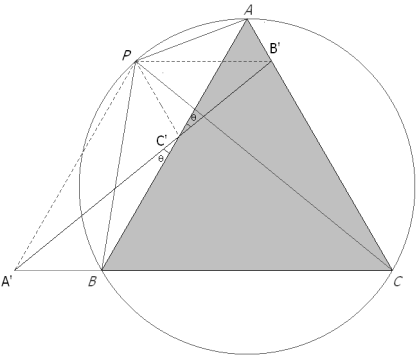
SI P ESTÁ SOBRE EL CÍRCULO CIRCUNSCRITO DEL TRIÁNGULO EQUILÁTERO ABC Demostraremos que en este caso, el triángulo de Pompeïu es degenerado (B, C’, A están alineados). Para ello consideraremos por separado BC’ y C’A.
Realizamos la misma construcción trazando por el punto P, sobre el círculo circunscrito, paralelas a los lados del triángulo equilátero. Observamos la parte inferior de la figura 9. Llamamos θ al ángulo del arco capaz de cuerda PA.
Por construcción, PC’BA’ es un trapecio isósceles y por lo tanto
Lo que haremos ahora es hallar el ángulo ∠AC’B’ usando la parte superior de la figura 10. Por tener los lados paralelos a ABC, los triángulos AC”B’ y PC’C” son equiláteros
vemos que los triángulos PC”A y C’C”B’ tienen dos lados y el ángulo que comprenden iguales por lo tanto los triángulos son congruentes y también tienen su tercer lado igual
lo que nos lleva a que el cuadrilátero PC’B’A es isósceles y por tanto es inscriptible. La cuerda AC, lado del triángulo equilátero, determina un arco capaz de 60° por lo tanto, en el triángulo PCA
y en el triángulo PCB’
entonces en el triángulo PB’A
y por tener la misma cuerda en el círculo circunscrito a PC’B’A
combinando [1] y [2]
y como AB es una recta fija, ∠A’C’B y ∠AC’B’ son ángulos opuestos por el vértice y además iguales y por lo tanto sus lados respectivos BC’ y C’A están en prolongación de ello deducimos que
luego el triángulo de Pompeïu, cuando P está sobre el círculo circunscrito, es degenerado. |
|
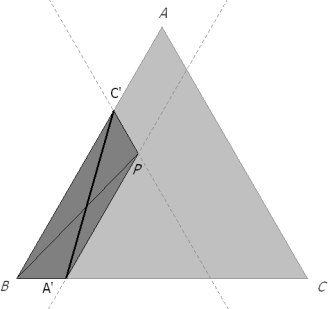
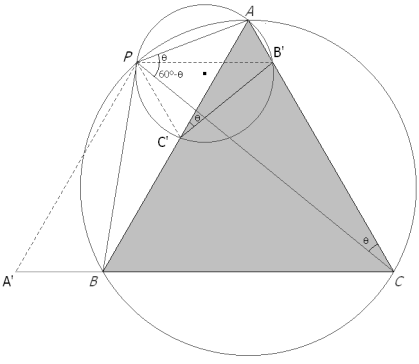
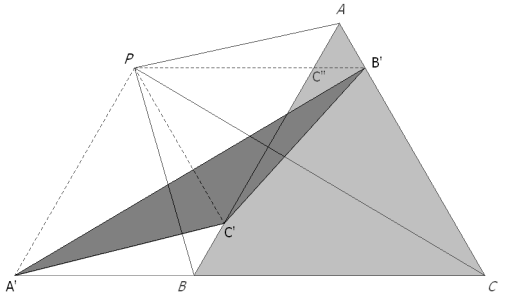
SI P ES UN PUNTO EXTERIOR AL TRIÁNGULO EQUILÁTERO ABC Por el punto P trazamos paralelas a los lados del triángulo equilátero ABC y seguimos formando trapecios; pero en algunas posiciones, las diagonales se transforman en lados; deberemos demostrar que el triángulo sigue siendo isósceles cosa que hemos hecho en el caso anterior y repetimos aquí.
El trapecio, en que los segmentos que nos interesan ocupan los lados no paralelos, es el PC’B’A (ver figura 12). Por tener los lados paralelos a ABC, los triángulos AC”B’ y PC’C” son equiláteros
vemos que los triángulos PC”A y C’C”B’ tienen dos lados y el ángulo que comprenden iguale;s por lo tanto, los triángulos son congruentes y también tienen su tercer lado igual
que es lo queríamos demostrar y por lo tanto, cuando P es exterior al triángulo equilátero ABC, sean PA, PB, PC diagonales o lados no paralelos de los trapecios formados, sigue persistiendo la construcción dada como solución. |
|
APÉNDICE |
|
En ABC, triángulo equilátero de lado l
la altura h es
y su radio circunscrito R
PROPOSICIÓN A Sea M un punto de coordenadas baricéntricas (r, s, t), en el plano de un triángulo cualquiera ABC,
entonces, se cumplirá
ya que
PROPOSICIÓN B - RELACIÓN DE LEIBNITZ PARA EL TRIÁNGULO Y para cualquier punto P del plano del triángulo se cumplirá
y sumando las tres ecuaciones, obtenemos (haciendo uso de la proposición A)
que es la relación de Leibnitz para el triángulo. PROPOSICIÓN C - EXPRESIÓN DE LA SUMA DE CUADRADOS DE DISTANCIAS ∑PA² Particularizando la relación de Leibnitz (proposición B)
y quitando denominadores
nos queda
En el triángulo equilátero
Y escribiendo PO=d, la [a] queda como
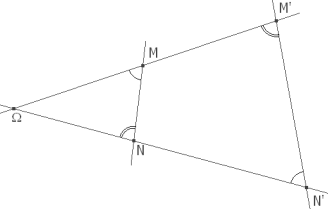
PROPOSICIÓN D - EFECTO DE UNA INVERSIÓN SOBRE LAS LONGITUDES A pesar de que una inversión (de centro Ω y razón k²) transforme rectas en círculos, si tenemos dos puntos M y N y sus inversos M’ y N’,
siempre podremos comparar las longitudes de MN y M’N’.
Si Ω es el centro de inversión, los triángulos ΩMN y ΩM’N’ son semejantes por el tipo de preservación de ángulos en la inversión. Luego
TEOREMA EXTENDIDO DE PTOLOMEO
Invertimos B, P, C respecto A y obtenemos B’, P’, C’. Entonces
que es una igualdad siempre que C’ esté sobre el interior del segmento B’C’. En una inversión de centro A y potencia k² un segmento cualquiera MN transforma su longitud en M’N’ tal que ([c])
y entonces
DEMOSTRACIÓN DEL TEOREMA DE POMPEÏU Del teorema extendido de Ptolomeo
como el triángulo ABC es equilátero BC=AB=AC=l
y realizando el mismo ejercicio de forma cíclica con cada punto
Que nos indica que PA, PB, PC son los lados de un triángulo Este triángulo es degenerado en el caso que los cuatro puntos se hallen sobre un círculo (o recta que no es nuestro caso) ya que tendremos tres posibles casos
CONSTRUCCIÓN DEL TRIÁNGULO DE POMPEÏU
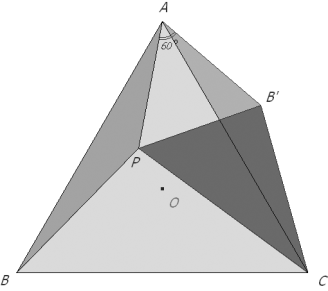
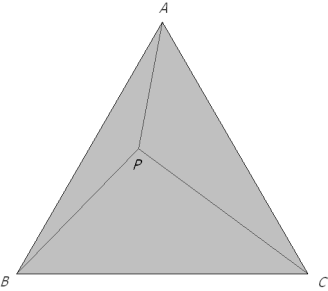
Cuando P es interior al triángulo, el triángulo de Pompeïu puede construirse fácilmente. Rotamos el triángulo APB en torno al vértice A un ángulo de 60° y obtenemos el triángulo AB’C, Ya que PA=B’A=PB' y PB=B'C, el triángulo de Pompeïu es PB'C. Esta construcción nos facilita el cálculo del área. EL ÁREA DEL TRIÁNGULO DE POMPEÏU 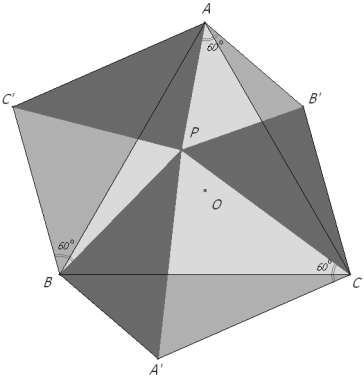
Si seguimos rotando, ahora el triángulo BPC, 60° con centro en B y el triángulo CPA, 60° con centro en C; obtenemos un exágono(ver figura 16), AB'CA'BC', donde los triángulos de Pompeïu PBA', PAC', PCB' tienen la misma área S. Y como
el área del hexágono que es
vale
pero también vale
donde APB’, BPC’, CPA’ son triángulos equiláteros y PCB’, PAC’, PBA’ son triángulos de Pompeïu con
por lo tanto igualando las dos expresiones del área del hexágono
que usando la ecuación [b], queda
|
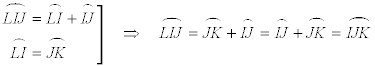
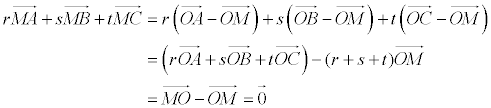 .
.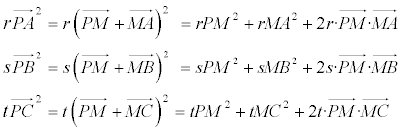
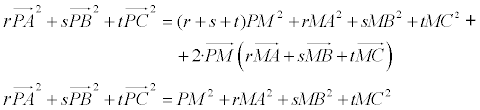
![[c] Ecuación 37](sol424ped/Eqn37.gif) [c]
[c]