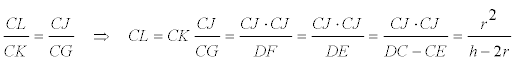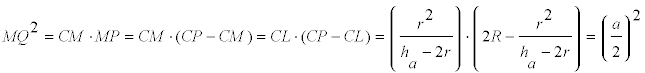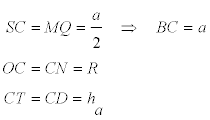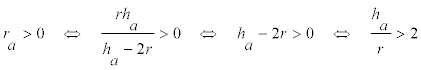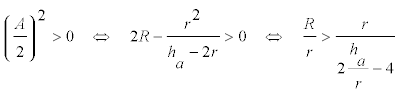|
De investigación. Propuesto por Vicente Vicario García, profesor del I.E.S. El SUR, Huelva Problema 425. Demostrar que es posible construir con regla y compás un triángulo ABC conocidos el radio de su circunferencia circunscrita R, el radio de su circunferencia inscrita r y una altura del mismo. Establecer también las condiciones para que sea posible tal construcción y proporcionar alguna. Vicario, V. (2007): Comunicación personal. Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (3 de diciembre de 2007) |
|
INTRODUCCIÓN |
|
|
Los problemas de construcción de un triángulo, dada una terna de datos, son muy comunes. De unos la construcción es directa, de otros más elaborada y de algunos imposible. Para la demostración que pide Vicente Vicario García, transformaremos este problema en otro más fácil; por ejemplo, podría ser el problema número 100 de las páginas de Ricardo Barroso; pero este problema todavía es algo “complicadillo” porque exige el empleo del radio del círculo inscrito. ¡ TRANSFORMAREMOS ESTE PROBLEMA EN EL DE CONSTRUIR UN TRIÁNGULO DADA LA BASE BC=a, LA ALTURA ha DESDE EL VÉRTICE A Y EL RADIO R DEL CÍRCULO CIRCUNSCRITO ! Como veremos una vez determinado a, este último problema se resuelve con las construcciones más elementales que hay en geometría. Exige un estudio detallado del triángulo para llegar de los datos del enunciado a los que nos permitirán la construcción final. Respecto a este estudio detallado del triángulo, debo agradecer unas observaciones de Francisco García Capitán que me han permitido simplificar algunas relaciones a usar (ver nº 400 extra Útiles simples para la resolución de problemas de triángulos apartados, 7.1 y 7.2). En primer lugar estableceremos nueve proposiciones previas, luego buscaremos los elementos de la construcción a partir de los datos del enunciado y estableceremos la solución. |
|
PROPOSICIONES PREVIAS |
|
|
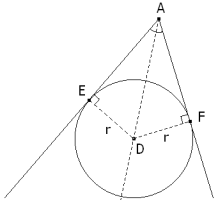
PROPOSICIÓN UNO Los segmentos que determinan los puntos de contacto del círculo inscrito en un ángulo y el vértice de dicho ángulo son iguales.
Al ser AD la bisectriz del ángulo A
Este resultado se puede obtener porque los triángulos AED y AFD tienen dos ángulos iguales, un lado igual y un lado común AD; lo que nos lleva a que el tercer lado de cada triángulo también es igual.
También podemos expresar la potencia del vértice A respecto al círculo inscrito y obtener la misma igualdad
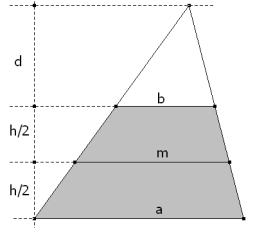
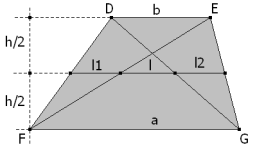
PROPOSICIÓN DOS La paralela a las bases en el punto medio de la altura (paralela intermedia) es igual a la semi-suma de las bases.
Expresamos d en función de la base mayor, la base menor y la altura
y ahora buscamos la relación para la paralela intermedia
PROPOSICIÓN TRES La distancia entre los puntos medios de las diagonales de un trapecio es igual a la semi-diferencia de las bases.
Observando los triángulos FDG y DFE, tenemos respectivamente las dos siguientes igualdades
y eliminando l1
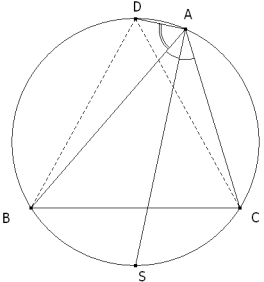
PROPOSICIÓN CUATRO En un triángulo cualquiera, la bisectriz corta al círculo circunscrito en el punto medio de los arcos que subtiende el lado opuesto al vértice.
Al ser AS la bisectriz del ángulo A tenemos
y como la igualdad de ángulos supone igualdad de arcos
Al ser AD la otra bisectriz del ángulo A
y como los ángulos son suplementarios, sus arcos, a lado distinto del diámetro, son iguales
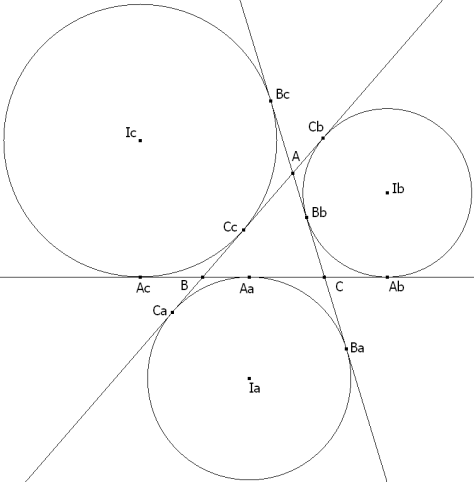
PROPOSICIÓN CINCO En un triángulo cualquiera, las distancia de un vértice a los puntos de contacto del círculo ex-inscrito opuesto a ese vértice son iguales al semi-perímetro.
Si dibujamos un triángulo de lados a, b, c y semi-perímetro p
con su círculo inscrito y sus círculos ex-inscritos y todos sus puntos de contacto notados según la figura tenemos
con la PROPOSICIÓN UNO
con la PROPOSICIÓN UNO, de nuevo
PROPOSICIÓN SEIS La distancia de un vértice al punto de contacto más próximo, fuera del triángulo es igual al semi-perímetro menos el lado del triángulo donde se encuentra el punto de contacto. Con la misma figura 5, y de acuerdo con la PROPOSICIÓN CINCO
del mismo modo
PROPOSICIÓN SIETE La distancia de un vértice al punto de contacto más próximo, dentro del triángulo es igual al semi-perímetro menos el lado del triángulo opuesto al vértice.
Si dibujamos un triángulo con su círculo inscrito y los puntos de contacto en cada laso
Y de acuerdo con la PROPOSICIÓN UNO
y así
con lo que
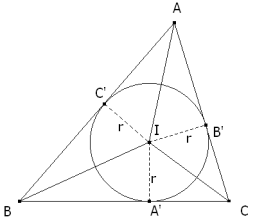
PROPOSICIÓN OCHO El área del triángulo es igual al producto del semi-perímetro por el radio del círculo inscrito. Si en la figura 6 observamos los radios perpendiculares a los lados y los segmentos de unión del incentro con los vértices, se forman tres triángulos con sus respectivas alturas y podemos escribir
PROPOSICIÓN NUEVE El área del triángulo es igual al producto del radio del círculo ex-inscrito opuesto a un vértice por el semi-perímetro menos el lado opuesto al mismo vértice.
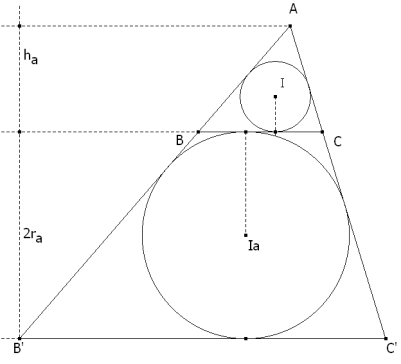
Destacando de la figura el radio del círculo inscrito y el círculo ex-inscrito, como los dos círculos son tangentes a los lados que concurren en el mismo vértice y los centros están alineados sobre la bisectriz que también pasa por el vértice, podemos decir que los dos círculos son homotéticos de centro A y la razón de homotecia será la razón de radios; por tanto los triángulos ABC y AB’C’ son homotéticos. En la misma homotecia y aprovechando la PROPOSICIÓN SIETE, podemos escribir
de donde
|
|
DESARROLLO DE LA SOLUCIÓN |
|
|
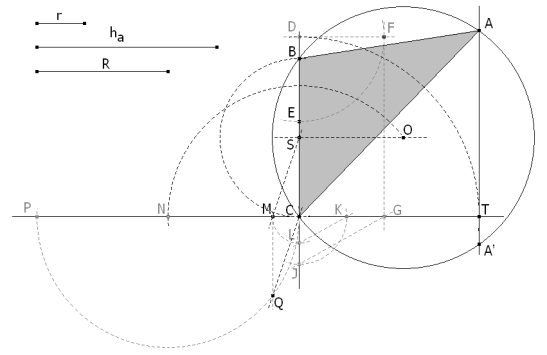
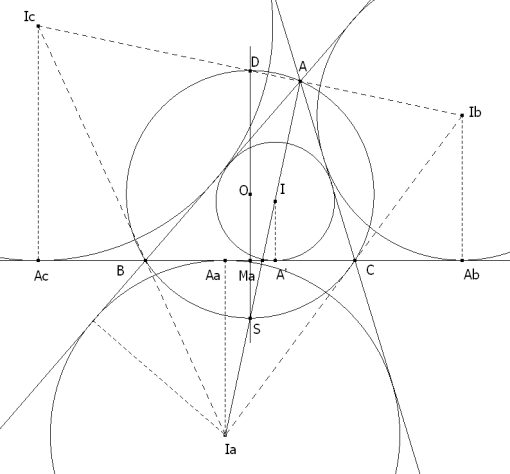
Ya que el enunciado nos proporciona R y r, dibujamos un triángulo con todos sus círculos.
Sea S el punto de intersección de la bisectriz AIa con el círculo circunscrito. Por la PROPOSICIÓN CUATRO, S es el punto medio del arco BSC. Sea D el punto de intersección del círculo circunscrito con la bisectriz AIb (además de A). Por la PROPOSICIÓN CUATRO, D es el punto medio del arco BDS. AIb , como bisectriz externa del ángulo A , es perpendicular a la bisectriz interna AIa ; lo que nos lleva a que el ángulo DAS es recto e inscrito en círculo circunscrito y por tanto DS es un diámetro de ese círculo; entonces S es el punto medio del arco BSC y en consecuencia DOS es perpendicular a BC y además perpendicular en el punto medio Ma de ese segmento. Pero teniendo en cuenta la PROPOSICIÓN CINCO,
y por eso, Ma es el punto medio de AcAb y ,en consecuencia, MaD es la paralela media del trapecio IbIcAcAb en el que aplicamos la PROPOSICIÓN DOS y obtenemos
De nuevo, con la PROPOSICIÓN SEIS y la PROPOSICIÓN SIETE
de lo que se desprende que Ma es el punto medio de AaA’ y como consecuencia S es el punto medio de IIa ; por tanto, MaS es el segmento de unión de los puntos medios de las diagonales del trapecio IA’IaAa ; por lo que podemos aplicar la PROPOSICIÓN TRES y escribir
y como DS es un diámetro del círculo circunscrito
Si calculamos la potencia del punto Ma respecto al círculo circunscrito (ver figura 8)
con lo que obtenemos el lado a
Observamos que necesitamos ra ; para ello aprovechando la PROPOSICIÓN OCHO y LA PROPOSICIÓN NUEVE
y de aquí
sustituyendo [2] en [1]
De donde con los datos del enunciado ya sabemos obtener a ; pero si simplificamos un poco, trabajaremos con segmentos menores y el dibujo no será tan farragoso.
|
|
LA CONSTRUCCIÓN |
|
|
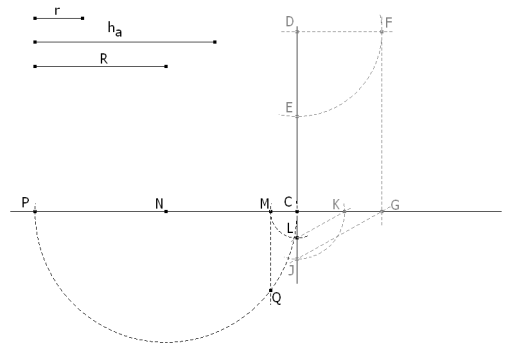
CONSTRUCCIÓN DE ( ra-r)/2=r2/(ha-2r)
CONSTRUCCIÓN DE a/2 (Ver ecuación [3])
CONSTRUCCIÓN DEL TRIÁNGULO
|
|
VALIDEZ DE LOS DATOS |
|
|
PRIMERA CONDICIÓN
SEGUNDA CONDICIÓN
|
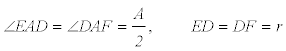
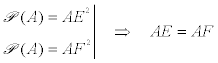
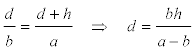
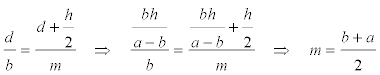
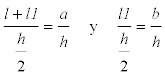
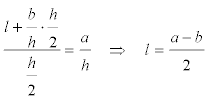
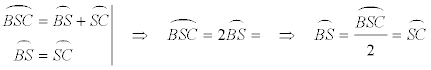
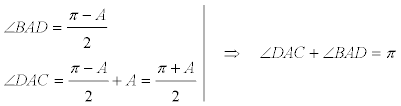
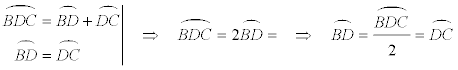
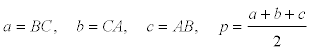
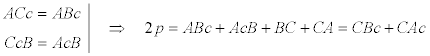
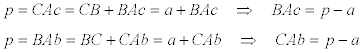
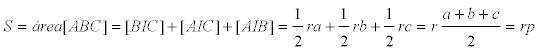
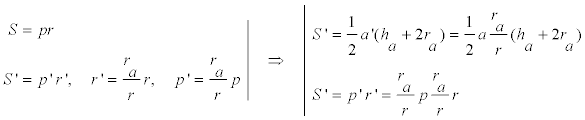
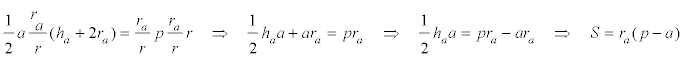
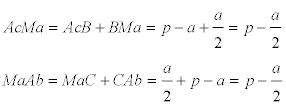
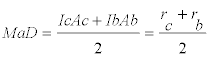
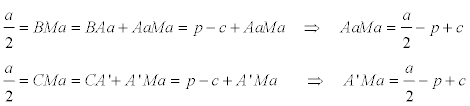
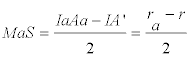
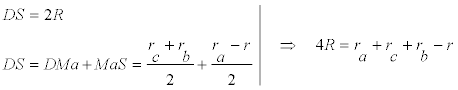
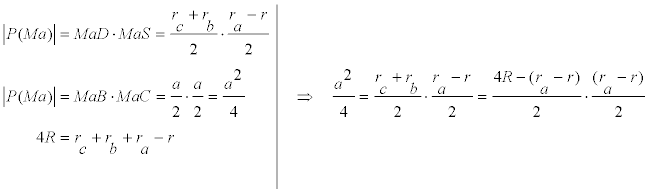
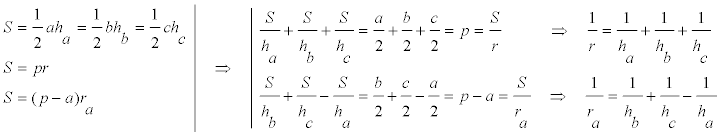
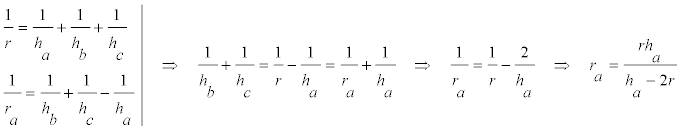 [2]
[2]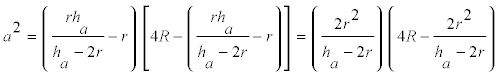
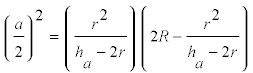 [3]
[3]