Problema 425

Demostrar que es posible construir con regla y compás un triángulo ABC conocidos el radio de su circunferencia circunscrita R, el radio de su circunferencia inscrita r y una altura del mismo. Establecer también las condiciones para que sea posible tal construcción y proporcionar alguna.

Vicario, V. (2007): Comunicación personal.

Resolución de Vicente Vicario García, I.E.S. “El Sur”, Huelva:

Un teorema básico sobre constructibilidad de segmentos con regla y compás afirma que si dos segmentos de longitudes y son constructibles, entonces también lo son los segmentos de longitudes , , , y .

Usaremos la notación habitual en la geometría del triángulo. Conocidos R y r, por el teorema de Euler, sabemos que la distancia circuncentro-incentro de un triángulo cumple la relación . Como corolario de esta igualdad tenemos la famosa desigualdad de Euler .

Sin pérdida de generalidad, podemos suponer conocida la altura , altura relativa al vértice A. Para esta altura tenemos la siguiente cadena de igualdades:

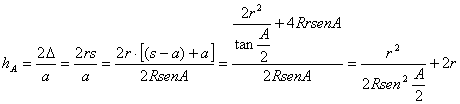[1]

donde hemos empleado las expresiones para el área del triángulo ABC y la expresión (teorema de los senos generalizado), la fórmula del seno del ángulo doble, además de la relación trigonométrica , con como la distancia del punto de contacto de la circunferencia inscrita al triángulo con el lado AC ó AB y el vértice A de mismo.

De la relación [1] deducimos que . Por otra parte, para la distancia entre el incentro I y el vértice A tenemos que

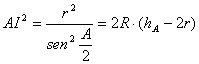[2]

ya que , por lo que podemos afirmar que es posible construir con regla y compás, un triángulo en las condiciones pdidas, puesto que AI es claramente un segmento constructible.

La construcción se efectúa construyendo las circunferencias de radios R y r con distancia entre sus centros de valor , que claramente es constructible con regla y compás. A continuación desde el incentro I como centro, se traza un arco de circunferencia hasta cortar a la circunferencia de radio R en los puntos simétricos A y A´. Finalmente por el teorema de los polígonos cerrados de Poncelet tenemos garantizado que desde cualesquiera de estos puntos A y A´ trazando tangentes a la circunferencia de radio r se cierra el polígono para formar el triángulo ABC pedido.

Nota: Las construcciones con regla y compás de los segmentos de longitudes y son sencillas y en el caso del primero bastaría con construir la longitud del lado del cuadrado del mismo área que el rectángulo de lados R y , lo cual se efectúa en la práctica uniendo los dos segmentos sobre una misma recta en un punto P limítrofe y observando que la perpendicular desde este punto corta a la semicircunferencia trazada con centro el punto medio del segmento unión de los dos y diámetro esta misma unión (teorema de la altura). Para la construcción de AI se procede de forma análoga con los segmentos de longitudes 2R y .