Problema 426
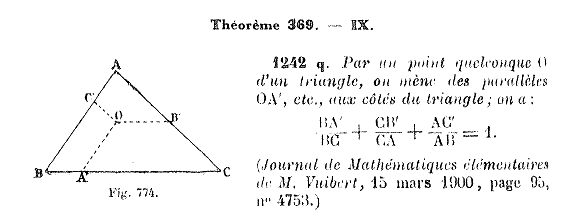
Teorema 369 Cuestión 1242. Por un punto cualquiera O de un triángulo, se toman paralelas OA’, etc, a los lados el triángulo; se tiene BA’/BC + CB’/CA + AC’/AB =1.
(Journal de Mathématiques élémentaires de M. Viubert, 15 de mars 1900, page 95, nº 4753.)
Frère Gabriel Marie, 1820-1891. 5. ed (1912). Exercices de géométrie, comprenant l'esposé des méthodes géométriques et 2000 questions résolues par F. G.-M.: 3 p. L., [iii]-xxiv, 1302 p. diagrs.
Solución del director
BA’/BC + CB’/CA + AC’/AB =1
(BA’ ha)/(BC ha ) + (CB’ hb)/(CA hb) + (AC’ hc) /(AB hc) =1
[BA’A]/ [ABC] + [CB’B]/[ABC]+[AC’C]/[ABC] =1
Al ser OA’ paralelo a AB, OB’ a BC y OC’ a AC, es:
[BA’A]= [BOA], [CB’B] =[COB], [AC’C]= [AOC]
Luego es:
[BA’A]/[ABC] + [CB’B]/[ABC]+[AC’C]/[ABC]= ([BOA]+ [COB]+[AOC])/[ABC].
Así, BA’/BC + CB’/CA + AC’/AB=[ABC]/[ABC]=1.