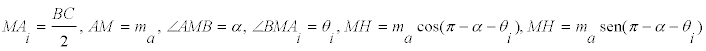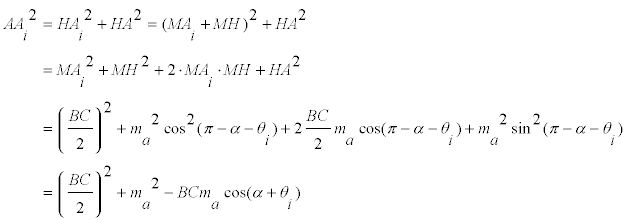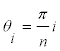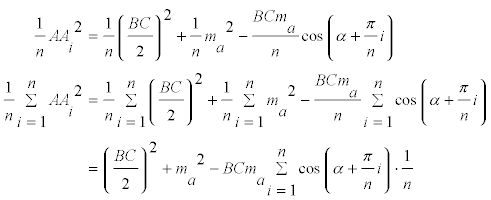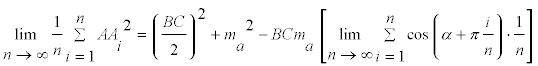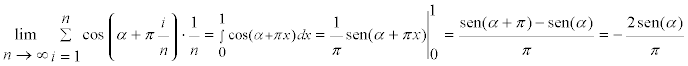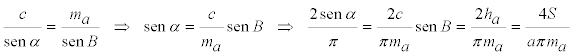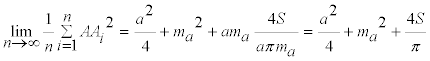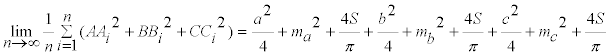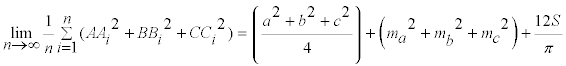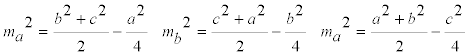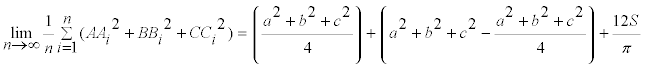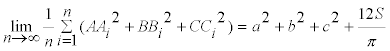EXTRA(5 diciembre 2007)

(En memoria de D. Jordi Dou, amante e impulsor de la cultura y recientemente fallecido).

Problema 427.-

Sea ABC un triángulo. Sobre cada uno de sus lados y exteriormente, construimos las semicircunferencias que tienen a sus lados como diámetros respectivos. Dividimos cada una de estas semicircunferencias en n arcos iguales. Determinar el límite del cociente de la suma de los cuadrados de las longitudes de los segmentos cuyos extremos son cada vértice del triángulo y cada uno de los puntos de división del arco opuesto entre el número n de arcos.

(Propuesto por Vicente Vicario García, I.E.S. “EL SUR”, Huelva).

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (6 de diciembre de 2007)

SOLUCIÓN

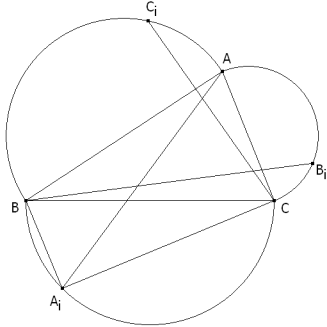
DIBUJO DEL ENUNCIADO

figura 1

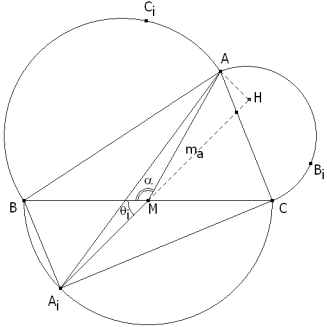
Démonos cuenta de que el razonamiento que hagamos para cualquier vértice sirve para los otros dos. Trabajaremos con el vértice A y adaptaremos los resultados a B y C.

figura 2

Observando la figura

Si seguimos observando

pero

y de aquí

pasando al límite cuando

pero

aplicando el teorema de los senos al triángulo BAM y al triángulo ABC (en función del circun-radio)

que nos lleva a

Podemos pues escribir

y ordenando

y expresando las medianas en función de los lados

nos queda

y simplificando