Problema 1.- (En memoria de D. Jordi Dou, amante e impulsor de la cultura y recientemente fallecido).

Sea ABC un triángulo. Sobre cada uno de sus lados y exteriormente, construimos las semicircunferencias que tienen a sus lados como diámetros respectivos. Dividimos cada una de estas semicircunferencias en n arcos iguales. Determinar el límite del cociente de la suma de los cuadrados de las longitudes de los segmentos cuyos extremos son cada vértice del triángulo y cada uno de los puntos de división del arco opuesto entre el número n de arcos.

(Propuesto por Vicente Vicario García, I.E.S. “EL SUR”, Huelva).

Resolución: (Vicente Vicario García, I.E.S. El Sur, Huelva)

Comenzaremos demostrando un lema que necesitaremos posteriormente. En la demostración aparecerá la forma exponencial euleriana para los números complejos e identidades trigonométricas clásicas.

Lema: “Si entonces se tienen las siguientes identidades trigonométricas:

”.

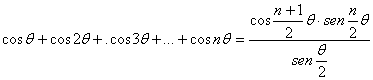
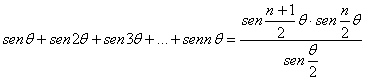Demostración: Definiremos T y S de la siguiente forma

Determinaremos el número complejoque vendrá dado por la expresión siguiente, aplicando la fórmula clásica para la suma de un número finito de términos de una progresión geométrica. También multiplicaremos y dividiremos por el complejo conjugado del complejo denominador para racionalizar la expresión y empleamos sucesivamente identidades trigonométricas conocidas.

de donde deducimos, igualando partes reales e imaginarias, respectivamente

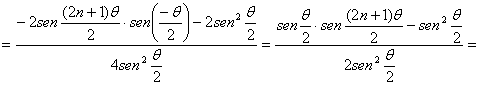
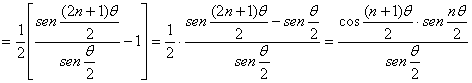
y a su vez, la parte imaginaria S vendrá dada por

■

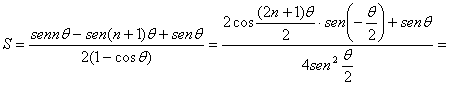
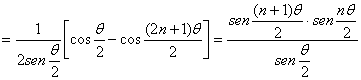Centrándonos ahora en el problema original, consideremos la semicircunferencia exterior al lado opuesto al vértice A del triángulo dado, dividida en n arcos iguales. Sea P el punto sobre dicha semicircunferencia que corresponde a la división i-ésima. Sea O el punto medio del lado BC, es decir, el centro de la semicircunferencia. Considerando el triángulo OPC, observamos que es isósceles y que el valor de los ángulos iguales en el mismo es

Por otra parte, la longitud del lado desigual PC en dicho triángulo isósceles, viene dada por

Consideremos ahora el triángulo APC y determinemos de forma genérica la distancia AP. Aplicando el teorema de los cosenos a dicho triángulo tenemos

y aplicando la identidad trigonométrica para el coseno de la suma de dos ángulos, junto con la expresión del coseno y el seno del ángulo C en función de los lados

Ahora, puesto que el área del triángulo ABC es , utilizando las expresiones trigonométricas del ángulo doble y del ángulo mitad, tenemos que la expresión anterior es igual a

Así pues, para la suma de todos los cuadrados de los segmentos que parten del vértice A del triángulo, tenemos

y resultado análogo para , , las sumas desde los vértices B y C.

Por otra parte, aplicando el lema anterior, tenemos que

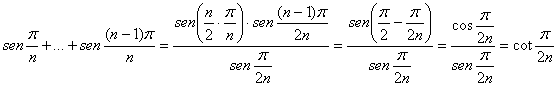
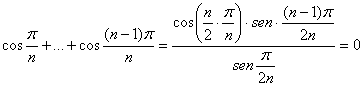
a partir de lo que obtenemos entonces

Finalmente, evaluamos la suma total

con lo que el límite pedido será

donde hemos aplicado, el hecho bien conocido de que , resultado que se puede deducir mediante consideraciones elementales sobre áreas de figuras en el círculo, o bien aplicando la regla de L´Hôpital.