EXTRA (11 diciembre 2007)

Problema 428.- Dedicado al profesor Jordi Dou.

Sea ABC un triángulo, AA´, BB´, CC´ son las bisectrices interiores que se cortan en el incentro I de los ángulos A, B, y C, respectivamente. Trazamos por B, y C, las perpendiculares a las bisectrices CC´, BB´, (prolongadas si es necesario) cortando a ellas, en los puntos M_a, N_a, respectivamente, y estas rectas se cortan en A_a. Sea P_a, el pie de la altura desde A_a sobre el lado BC. Probar que:

El triángulo M_aN_aP_a (que es el triángulo órtico del triángulo A_aBC) es inversamente semejante al triángulo ABC, cuyo incentro I coincide con el ortocentro del triángulo A_aBC. Hallar los elementos de la semejanza.

Romero, J.B. (2007): Comunicación personal.

Solución de Saturnino Campo Ruiz, profesor del IES Fray Luis de León, de Salamanca.

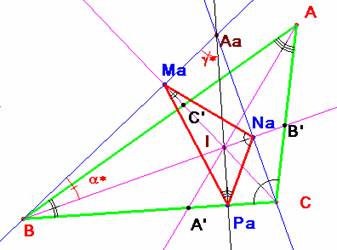
Vamos a llamar a, b y g a los ángulos del triángulo ABC y a*, b* y g* a los ángulos mitad de aquéllos cuya suma es un recto.

Observando la figura vemos que los ángulos BA_aP_a y M_aCB = g* son iguales por tener sus lados perpendiculares. Por tanto, el ángulo A_aBP_a es el complementario de g*, de donde A_aBI = a* y en consecuencia, el ángulo IA_aN_a es igual a b*.

En resumen, para el triángulo A_aBC, los ángulos en cada vértice miden b*+g* =90- a*, b* + a* = 90- g* y a* + g* = 90- b* respectivamente.

Además, sus alturas son bisectrices del triángulo órtico. Por eso el ángulo en M_a es igual para el triángulo BM_aP_a, que contiene al vértice B que para el A_aM_aN_a, que contiene a A_a. E igual en los demás. Un cómputo de estos ángulos nos lleva a deducir que el triángulo órtico de un triángulo cualquiera determina sobre él otros tres triángulos semejantes (inversamente) al original.

En particular M_a mide a*+g* = 90- b*. Con este dato calculamos para el triángulo M_aN_aP_a que el ángulo N_aM_aP_a = 180- 2(90- b*) = b.

El mismo procedimiento nos da que áng(M_aN_aP_a)= g quedando, con esto, establecida la semejanza entre los triángulos ABC y M_aN_aP_a. Se corresponden (P_a ,M_a ,N_a) con (A, B, C).

El recorrido de los vértices de uno de ellos tiene sentido antihorario, y el de los homólogos en el otro antihorario, como corresponde a una semejanza inversa.

Tomando el triángulo A_aN_aP_a, la semejanza con A_aBC establece la correspondencia de vértices homólogos (A_a , M_a , N_a) à(A_a, C, B). Calculemos la razón de semejanza. En CM_aA_a se tiene que A_a M_a = A_a C· cos (90- a*). Por tanto la razón es el valor del coseno: cos (90- a*) = sen a*, y entonces, sen a*, y esa es también la razón de semejanza entre los dos triángulos del enunciado.