Problema 428. (Dedicado al profesor D. Jordi Dou).

Sea ABC un triángulo, AA´, BB´, CC´ son las bisectrices interiores de los ángulos A, B, C respectivamente, que se cortan en el incentro I. Trazamos por B y C las perpendiculares a las bisectrices CC´ y BB´ (prolongar si fuese necesario) cortándolas en los puntos y , respectivamente, y éstas se cortan en . Sea el pie de la altura desde sobre el lado BC. Probar que: El triángulo ,, (que es el triángulo órtico del triángulo ) es inversamente semejante al triángulo ABC, cuyo incentro coincide con el ortocentro del triángulo. Hallar los elementos de la semejanza.

(Propuesto por J. Bosco Romero Márquez, Universidad de Valladolid).

Resolución: (Vicente Vicario García)

Comenzaremos demostrando un lema asociado con el triángulo órtico de cualquier triángulo acutángulo:

Lema: “Sea ABC un triángulo acutángulo, entonces su triángulo órtico de vértices A´, B´, C´ situados respectivamente sobre los lados opuestos a los vértices A, B, C del triángulo ABC, tiene como longitudes de sus lados , ,. Además se cumplen las relaciones angulares siguientes

, , ”.

Demostración: Consideremos, sin pérdida de generalidad, los vértices B´ y C´ del triángulo órtico. Claramente, a partir del triángulo rectángulo , rectángulo en B´ tenemos que . En el triángulo rectángulo , rectángulo en C´, de forma análoga tenemos que . Aplicando ahora el teorema de los cosenos al triángulo AB´C´ tenemos

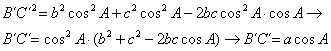
y análogamente para los lados A´C´ y A´B´, lo que demuestra la primera parte del lema. Podemos ver también que los triángulos AB´C´, BA´C´ y CA´B´ son semejantes al triángulo ABC original (por tener los tres lados proporcionales), con lo que es fácil obtener ahora las igualdades entre los ángulos siguientes: , , ■

Volviendo al problema original, siendo I el incentro del triángulo ABC, es fácil verificar la relación angular siguiente

.

Entonces, debido a la construcción, tenemos claramente que , , por ser ángulos suplementarios de . Además, tenemos que y son opuestos por el vértice. Por tanto, y , por ser , triángulos rectángulos. Además, el triángulo es acutángulo, ya que

y análogamente

y entonces tiene sentido hablar de triángulo órtico del triángulo .

Por otra parte, por construcción y , entonces CC´ y BB´ son alturas del triángulo y, por tanto, deducimos entonces que la altura debe pasar también por el punto de corte de las otras dos, es decir, por el incentro I del triángulo ABC. Utilizando las relaciones angulares obtenidas en el lema y aplicándolas al triángulo acutángulo , se obtienen inmediatamente las relaciones angulares , , , con lo que los triángulos y ABC son semejantes por tener los tres ángulos iguales. Observamos además que la semejanza es inversa ya que ningún giro de centro el incentro I sitúa en posición nomotética a los triángulos anteriores.

Por otra parte, utilizando el lema podemos determinar fácilmente la razón k de semejanza ya que

y en consecuencia, la relación entre lados homólogos proporciona

,

---oooOooo---