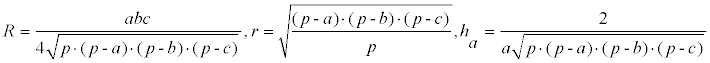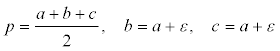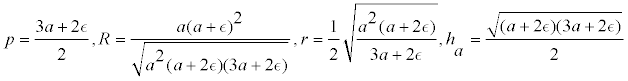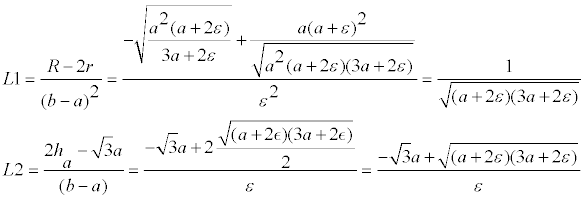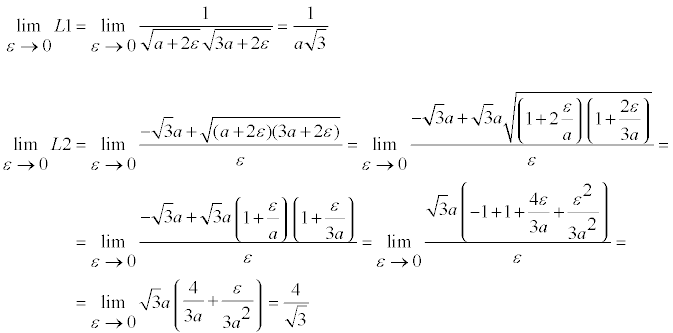De investigación

Propuesto por Juan Bosco Romero Márquez, profesor colaborador de la Universidad de Valladolid

Problema 431

Sea ABC un triángulo isósceles, en A, con la base a, fija, y b=c variable. Sean r, R, el radio del círculo inscrito y circunscrito, respectivamente, y ha, la altura correspondiente al lado a.

Calcular los siguientes límites cuando b tiende a, es decir, cuando el triángulo isósceles tiende a equilátero:

.

Romero, J.B. (2008): Comunicación personal.

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (6 de diciembre de 2007)

SOLUCIÓN

Expresemos R, r, h_a en función de los lados y el semi-perímetro.

pero podemos expresar el semi-perímetro p y los lados b y c en función de a

y nos queda

que llevado a las expresiones del enunciado dan

Pero si b tiende hacia a significa que ε tiende hacia cero

donde en el segundo límite hemos sustituido la raíz cuadrada por su infinitésimo equivalente.
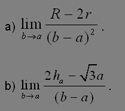