Problema 431. (Propuesto por J. B. Romero Márquez, profesor colaborador de
Sea ABC un triángulo isósceles, en A, con la base fija a y 
variable. Sean r, R los radios de las circunferencias inscrita y circunscrita al triángulo ABC, respectivamente y 
, la altura correspondiente al lado a. Calcular los siguientes límites cuando b tiende hacia a, es decir, cuando el triángulo isósceles tiende a equilátero
(a) 
(b) 
Resolución: (Vicente Vicario García, Huelva)
Utilizaremos la notación habitual en la geometría del triángulo. Comenzaremos por determinar los valores de r y R en función de los lados del triángulo con la hipótesis(triángulo isósceles).
El semiperímetro s del triángulo viene dado por 
. Por otra parte, de la conocida relación 
, donde
es el área del triángulo, tenemos que
donde hemos aplicado el teorema de Pitágoras para obtener en función de los lados.
Por otra parte, a partir del teorema de los senos generalizado aplicado al triángulo ABC, podemos obtener el valor de R de manera que
y a partir del teorema de los cosenos, aplicado al mismo triángulo, el valor de 
en función de los lados
de forma que el radio R de la circunferencia circunscrita viene dado por
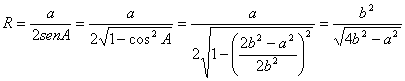
Entonces, ya podemos sustituir para calcular el valor del límite pedido
(a)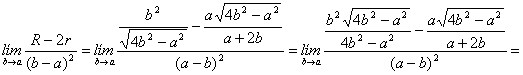 
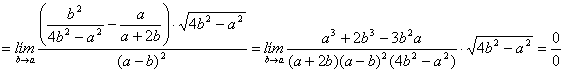
Para salvar la indeterminación es conveniente descomponer en factores el polinomio numerador mediante la regla de Ruffini, para después simplificar factores comunes. El límite anterior nos queda
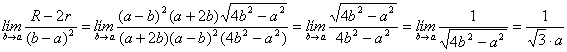
Para el segundo límite, sustituyendo el valor anterior de en función de los lados del triángulo, tenemos que
(b)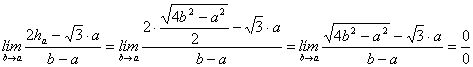 
A partir de aquí, y para salvar de nuevo la indeterminación, resolveremos el límite de dos formas diferentes. En la primera, aplicaremos la conocida regla de L´Hôpital y en la segunda, multiplicaremos y dividiremos por expresión radical conjugada.
(1)
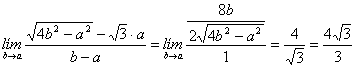(L´Hôpital)
(2)
