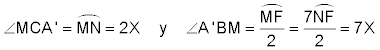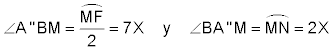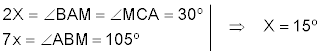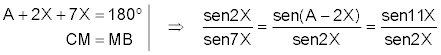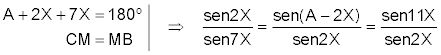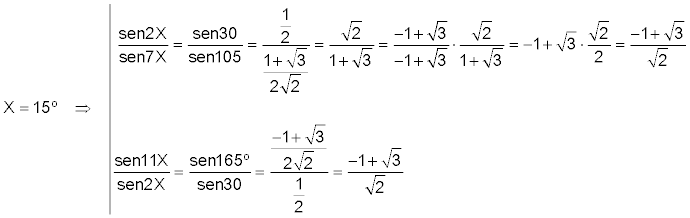De investigación. Propuesto por Alejandro Cipriano Coronel, estudiante universitario de ingeniería de la UNASAM (UNIVERSIDAD NACIONAL SANTIAGO ANTÚNEZ DE MAYOLO), Huaraz-Ancash-PERÚ.

Problema 432. En un triángulo ABC se traza la mediana AM relativa a BC (M en BC); además la medida de los ángulos ∠BAM=∠MCA=2X y ∠ABM=7X. Halle X.

Ubaldo, Luis. Triángulos II

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (16 de enero de 2008)

SOLUCIÓN

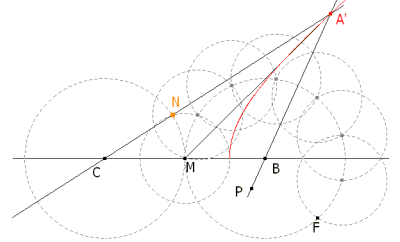
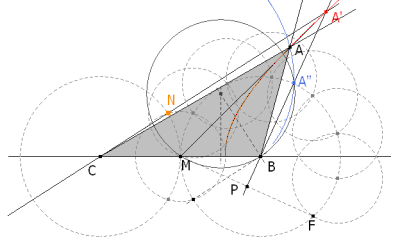
Fijaremos BC, obtendremos el vértice A como intersección de dos lugares, mediremos los ángulos obtenidos y realizaremos luego una comprobación trigonométrica.

PRIMER LUGAR

figura 1

• Tomamos C sobre una recta que pasa por M y trazamos el círculo de centro C que pasa por M.
• Trazamos el círculo de centro B que pasa por M, donde B es el simétrico de C respecto a M.
• Sobre el círculo de centro C tomamos un punto N y trazamos el círculo de centro M que pasa por N.
• Este último círculo corta el círculo de centro B en un punto que será el centro de un nuevo círculo que pasa por el punto M.
• Este último círculo vuelve a cortar el círculo de centro B en un punto que será el centro de un nuevo círculo que pasa por el centro del círculo acabado de dibujar.
• Repetimos la operación hasta obtener siete círculos. El séptimo círculo vuelve a cortar al círculo de centro B en el punto F.
• Trazamos P punto medio de MF.
• Trazamos CN y BP que se cortan en A’ (en rojo).

Esta construcción asegura que

Pedimos a CABRI II el lugar geométrico de A’ cuando desplazamos N sobre el círculo de centro C.

La curva obtenida (en rojo) es el lugar del vértice de los triángulos de base BC fija y ángulos ∠MCA’=2X y ∠A’BM=7X.

SEGUNDO LUGAR

figura 2

• Sobre el segmento BM trazamos el arco capaz de ángulo MN=2X.
• BP corta al arco capaz en A” (en azul).

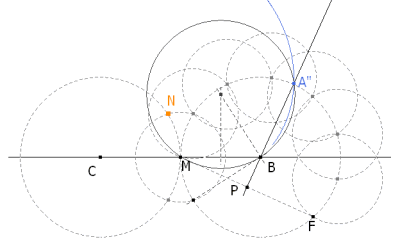
Esta construcción asegura que

Pedimos a CABRI II Plus el lugar geométrico de A” cuando desplazamos N sobre el círculo de centro C.

La curva obtenida (en azul) es el lugar del vértice de los triángulos de semi-base CM fija y ángulos ∠BA”M=2X y ∠A”BM=7X.

EL TRIÁNGULO PEDIDO

figura 3

Trazamos simultáneamente los dos lugares que se cortan en A (en negro). El triángulo ABC así obtenido es el pedido pues cumple

figura 4

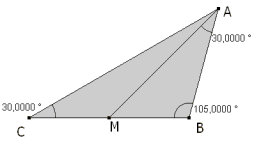
Medimos los ángulos con CABRI II Plus y obtenemos los datos de la figura.

Lo que significa que

COMPROBACIÓN

Aplicando el teorema de los senos

dividiendo miembro a miembro las dos igualdades

que en nuestro caso queda

que nos demuestra que el valor de X=15º es correcto.