Problema 432. (Propuesto por Alejandro Cipriano Coronel, estudiante universitario de ingeniería de
En un triángulo ABC se traza la mediana AM relativa a BC (M en BC), además la medida de los ángulos 
y 
. Hallar X.
Resolución: (Vicente Vicario García, Huelva)
Supondremos para mayor comodidad y sin pérdida de generalidad que 
. De forma trivial obtenemos también las relaciones angulares siguientes:
, 
, 
.
Aplicando el teorema de los senos al triángulo ABM tenemos
Aplicando el teorema de los senos al triángulo AMC tenemos
Igualando ahora las dos expresiones obtenidas para AM entonces
Tenemos que resolver la ecuación trigonométrica anterior. Una de sus soluciones es la trivial 
. Además, para sus posibles soluciones reales positivas es evidente que tenemos la acotación trivial 
(rad) que se obtiene al aplicar la relación angular clásica al triángulo ABC.
Demostraremos que la única solución admisible para nuestro problema (que cumple la restricción anterior) es la que corresponde a
rad =15º.
Para la demostración, efectuaremos algunos cálculos trigonométricos. Comenzaremos por determinar el valor exacto de 
y 
utilizando las expresiones trigonométricas para suma y diferencia de ángulos.
Por otra parte ya es sencillo determinar 
y 
ya que
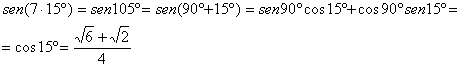
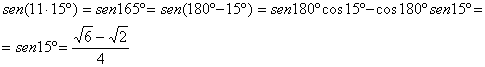
Entonces es fácil determinar
Finalmente, basta observar que
Un razonamiento rutinario sobre continuidad y derivabilidad de la función 
, demuestra que existe un único cero real positivo de esta función en el intervalo 
. Así pues, hemos demostrado que 
es la única solución admisible de la ecuación trigonométrica 
compatible con nuestro problema geométrico.