Problema 433. Demostrar la veracidad de las siguientes proposiciones:

(a)   En todo triángulo ABC se verifica la desigualdad

(b)   En todo triángulo acutángulo ABC se verifica la desigualdad

Resolución: (Vicente Vicario García, Huelva)

            Para demostrar (a) manipulamos algebraicamente y llegamos a la desigualdad equivalente

Deduciremos ahora un lema importante que nos permitirá determinar los sumando de la desigualdad anterior.

Lema: “Con la notación habitual para un triángulo sea A un ángulo del mismo, entonces  cosA  es una raíz real de la ecuación polinómica  siguiente:

 ”.

Para la demostración consideremos las relaciones  (teorema de los senos generalizado) y  (relacionada con el incentro). Tenemos que utilizando las identidades trigonométricas del ángulo doble

Elevando al cuadrado y operando se tiene

           

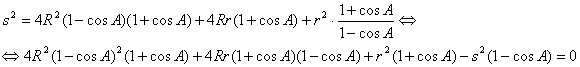
de donde, después de manipulaciones algebraicas, llegamos a la relación que queremos

Claramente esta relación se cumple también para  y . De las relaciones de Cardano-Vieta entre las raíces y los coeficientes deducimos las relaciones

                            

            Llevando estas relaciones a la desigualdad entonces

y esta última desigualdad es cierta ya que es una del grupo de las denominadas desigualdades de J. C. Gerretsen, y de la cual se puede encontrar una demostración en mi artículo “Caracterización del triángulo HIO” del número extra de esta revista.

            Para demostrar (b) necesitamos tres lemas de demostración muy sencilla

Lema 1: “Para todo triángulo ABC se tiene ”

            Para su demostración basta observar que , tomar tangentes en los dos miembros y utilizar la expresión para la tangente de la suma de dos ángulos y relaciones trigonométricas entre ángulos suplementarios.

Lema2:“Para todo triángulo ABC se tiene ”

            Para su demostración basta observar que , tomar cotangentes en los dos miembros y emplear la expresión para la cotangente de la suma de dos ángulos y relaciones trigonométricas entre ángulos complementarios.

Lema3: “Para todo ángulo se tiene ”

            Para la demostración basta utilizar la clásicas expresiones de la tangente del ángulo mitad

                                  

            Finalmente la demostración ya es inmediata porque tenemos

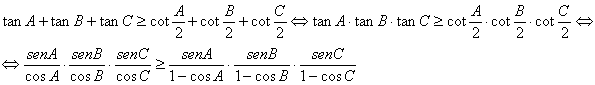
            Y como el triángulo es acutángulo los cosenos de sus ángulos son positivos y la desigualdad anterior se transforma en la del apartado (a) anterior que ya demostramos que es cierta.