PROBLEMA 434
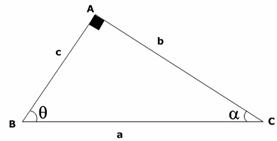
Sea un triángulo rectángulo en A, de hipotenusa a, catetos b y c, semiperímetro p y área S.
1. Calcular los catetos en función de la hipotenusa y el área.
2. Demostrar geométricamente que si los ángulos agudos son de 15º y 75º, el producto de los catetos es equivalente al cuadrado de la mitad de la hipotenusa.
3. Hallar los ángulos sabiendo que:![]()
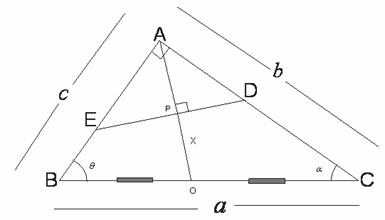
4. Sea M el punto medio de la altura por A. Se traza por M una recta DE cuyo punto medio es M, y está limitada por los catetos. Se pide el valor de los ángulos en E y D en función de los del triángulo.
5. Trazada la perpendicular por A a esta recta DE, determinar la distancia OP siendo P el punto de intersección de dicha perpendicular con la hipotenusa y O el punto medio de la hipotenusa.
Pedret, J. M. (2007): Comunicación personal.
Solución (1) Pide los catetos en función de la hipotenusa y el área
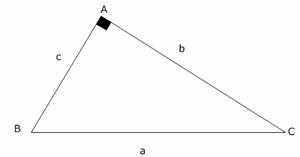
En el triángulo rectángulo se cumple el Teorema De Pitágoras: ![]() … (*)
… (*)
Además se sabe que el área: 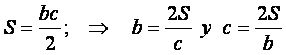
CÁLCULO DEL CATETO (b)
Sumando miembro a miembro (m. a. m.) “2bc” en la ecuación (*) se tiene: ![]() Entonces
Entonces ![]() ; pero bc = 2S; Entonces
; pero bc = 2S; Entonces
![]() ……. (**)
……. (**)
Ahora en esta expresión reemplacemos el valor de “c” y tendremos: ![]() operando se obtiene:
operando se obtiene: ![]() y
y
Resolviendo la ecuación se llega a los valores de “b”: 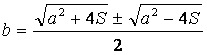
como podemos observar “b” toma 2 valores y ambos son positivos, por lo tanto se acepta ambos valores.
CÁLCULO DEL CATETO (c)
Con los mismos procedimientos realizados en el cálculo de “b” se obtiene lo siguiente:
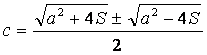 Éste también toma dos valores y ambos son positivos por lo tanto se aceptan los dos valores.
Éste también toma dos valores y ambos son positivos por lo tanto se aceptan los dos valores.
A simple vista se puede concluir que “b = c”; pero de la ecuación (**) por simple inspección podemos concluir que “b” debe ser diferente de “c” o sea si:
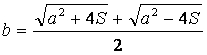 Entonces
Entonces 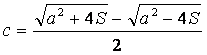 y si
y si
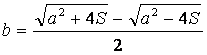 Entonces
Entonces 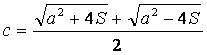
Estos serían las respuestas.
Solución (2)
Se traza la altura AH (relativo a la hipotenusa), luego se traza la mediana AM (relativo a la hipotenusa), se sabe que en un triángulo rectángulo la mediana relativa a la hipotenusa mide la mitad de dicha hipotenusa. O sea (BC = MC = AM = a/2); entonces si BC mide “a”; por lo tanto la mediana medirá “a/2”; además el triángulo AMC es isósceles (AM = MC, m< MAC = m< MCA = 15º) entonces la medida del ángulo AMB será 30º.
Luego en el triángulo rectángulo notable AHM (30º, 60º) se cumple que el cateto opuesto a 30º mide la mitad de la hipotenusa o sea “a/4”. Con esto se está demostrando que “la altura mide la cuarta parte de la hipotenusa”.
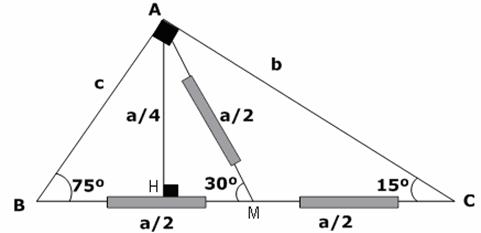
Finalmente sabemos por relaciones métricas en un triángulo rectángulo se cumple:
EL PRODUCTO DE LOS CATETOS ES IGUAL AL PRODUCTO DE LA ALTURA (Relativo A La Hipotenusa) Y LA HIPOTENUSA.
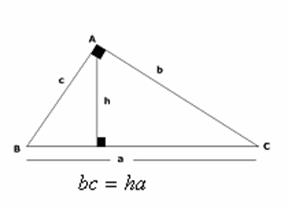
Entonces del problema se tiene que: 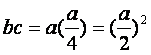
Por la tanto: 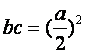 …… LQQD.
…… LQQD.
Solución 3
Sean ![]() los ángulos.
los ángulos.
Se sabe que: 2P = a+ b+ c y por dato se sabe que: 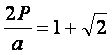 reemplazando 2P se tiene
reemplazando 2P se tiene 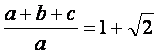 ; entonces
; entonces 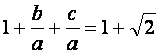 cancelando 1 m.a. m. se tiene:
cancelando 1 m.a. m. se tiene: 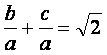 …… (1)
…… (1)
Pero es claro que 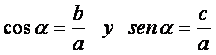 reemplazando estos valores en (1) se tiene:
reemplazando estos valores en (1) se tiene: ![]() elevando al cuadrado m.a m. Se tiene
elevando al cuadrado m.a m. Se tiene
![]() Aplicando identidad pitagórica se tiene:
Aplicando identidad pitagórica se tiene: ![]() y por arcos dobles se tiene:
y por arcos dobles se tiene: ![]()
![]() Y de ahí se tiene que:
Y de ahí se tiene que: ![]()
Por lo tanto el ángulo ![]() ya que la suma de estos ángulos debe ser 90º
ya que la suma de estos ángulos debe ser 90º
![]() Y
Y ![]() …. RPTAS.
…. RPTAS.
Solución 4
De acuerdo a los datos se tiene la siguiente gráfica y sea X e Y los ángulos que se pide calcular en función de los ángulos del triángulo.
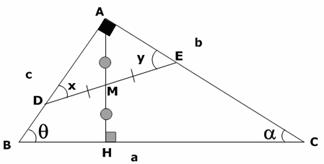
Se une los puntos H con A, C con H; así obteniendo el cuadrilátero ADHE.
Luego se observa que el triángulo DMA es congruente HME (DM = ME; AM=MH; m< AMD = m< EMH); Entonces m< ADE = m< DEH = X y m< DAH=m< AHE=![]() con esto se demuestra que AB//EH
con esto se demuestra que AB//EH
Además el triángulo DMH es congruente con AME (DM = ME; AM = MH;
m< AED = m< EDH = Y); Entonces m< EAH =m< AHD = ![]() .
.
Con todo esto se esta demostrando que el cuadrilátero ADHE tiene los ángulos rectos; entonces sus diagonales son iguales.
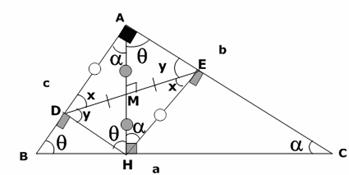
Y como estos diagonales se cortan en sus puntos medios se tiene que:
X = ![]() y Y =
y Y = ![]() ……. RPTAS.
……. RPTAS.
Con estos resultados también se ha demostrado que el cuadrilátero es un CUADRADO. Ya que X = ![]() por lo tanto en el triángulo DMA se cumple que M es un ángulo recto (90º). Es por eso que el cuadrilátero ADHE es un cuadrado.
por lo tanto en el triángulo DMA se cumple que M es un ángulo recto (90º). Es por eso que el cuadrilátero ADHE es un cuadrado.
Solución 5
Pide PO = X ; pero sabemos que P y M son el mismo punto, por el problema anterior.(EM = MD o EP = PD). Y también AM = MO ó AP = PO = X
Además AO es perpendicular a BC, O (recto).
O sea que AO es una mediana y altura; dicha mediana es la mitad de la hipotenusa.
Entonces 2X = a/2 de donde se tiene que: X = a/4..... RESPUESTA.