Problema 434 de triánguloscabri

Para el aula

Sea un triángulo rectángulo en A, de hipotenusa a, catetos b y c, semiperímetro p y área S.

  1. Calcular los catetos en función de la hipotenusa y el área.
  2. Demostrar geométricamente que si los ángulos agudos son de 15º y 75º, el producto de los catetos es equivalente al cuadrado de la mitad de la hipotenusa.
  3. Hallar los ángulos sabiendo que .
  4. Sea M el punto medio de la altura por A. Se traza por M una recta DE cuyo punto medio es M, y está limitada por los catetos. Se pide el valor de los ángulos en E y D en función de los del triángulo.
  5. Trazada la perpendicular por A a esta recta DE, determinar la distancia OP siendo P el punto de intersección de dicha perpendicular con la hipotenusa y O el punto medio de la hipotenusa.
Propuesto por José María Pedret. Ingeniero Naval.

Solución de Francisco Javier García Capitán

1. Calcular los catetos en función de la hipotenusa y el área.
 

Por un lado tenemos y por otro, por lo que y son las soluciones de la ecuación , es decir
2. Demostrar geométricamente que si los ángulos agudos son de 15º y 75º, el producto de los catetos es equivalente al cuadrado de la mitad de la hipotenusa.
 

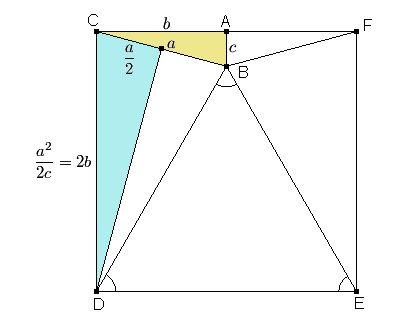Los dos triángulos rectángulos coloreados de la figura tienen ángulos de 15º y 75º. Entonces el cuadrilátero CDEF resulta ser un cuadrado y el triángulo BDE es equilátero.

El resultado es inmediato.

 

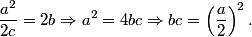
3. Hallar los ángulos sabiendo que .
 

Según la hipótesis es

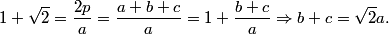
Por otro lado, usando la desigualdad entre las medias aritmética y cuadrática,

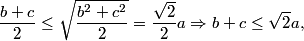
cumpliéndose la iugaldad si y solo si b y c son iguales. Por tanto, en nuestro caso tendremos que b=c=45º.
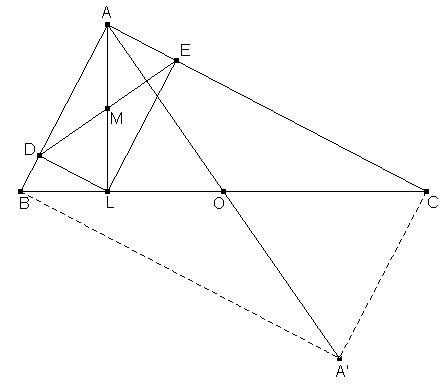
4. Sea M el punto medio de la altura por A. Se traza por M una recta DE cuyo punto medio es M, y está limitada por los catetos. Se pide el valor de los ángulos en E y D en función de los del triángulo.
 

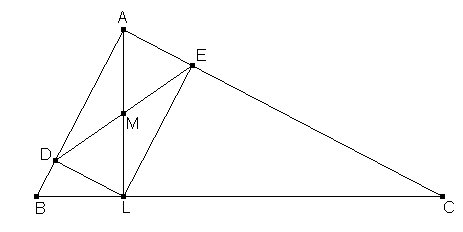
Refiriéndonos a la figura, por ser M el punto medio de la altura AL y del segmento DE tenemos la igualdad vectorial AD = AM + MD = ML + EM = EM + ML = EL, e igualmente DL = AE, por lo que ADLE es un paralelogramo, y por tanto un rectángulo. En el triángulo ADE tenemos los ángulos ÐADE = ÐADM = ÐMAD = ÐLAB = ÐC, y ÐAED = ÐB.
5.

Trazada la perpendicular por A a esta recta DE, determinar la distancia OP siendo P el punto de intersección de dicha perpendicular con la hipotenusa y O el punto medio de la hipotenusa.
 
  Si llamamos A' al simétrico de A respecto de O, obtendremos el rectángulo ABA'C semejante a AELD. Como los lados homólogos, por ejemplo AB y AE, de estos triángulos son perpendiculares, también lo serán sus diagonales, por ejemplo, DE y AA', por lo que la perpendicular a DE por A pasa por O y la distancia pedida es cero.