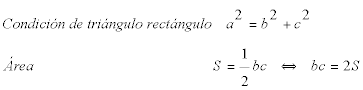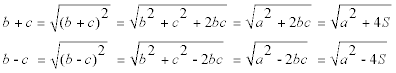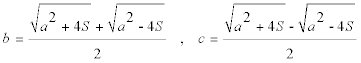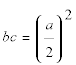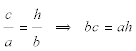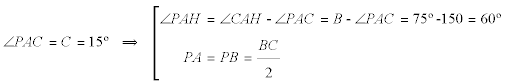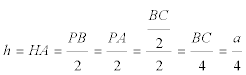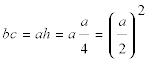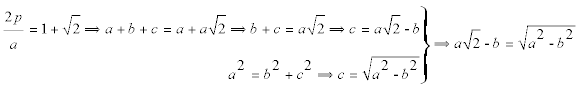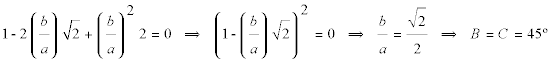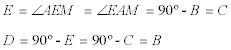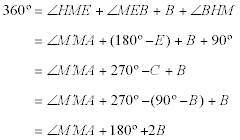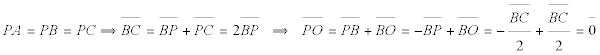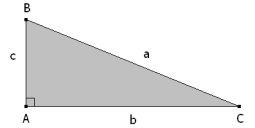
Calcular los catetos en función de la hipotenusa y del área.

figura 1

... calculamos

y obtenemos

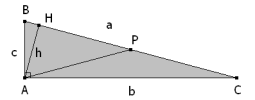
Demostrar geométricamente que si los ángulos agudos son 15° y 75° el producto de los catetos es equivalente al cuadrado de la mitad de la hipotenusa.

figura 2

Nos piden que demostremos

Si trazamos la altura por A, los triángulos ABC  y HAC  son semejantes, pues tienen tres ángulos iguales, y podemos escribir

Si trazamos P  sobre BC  tal que AP = BP, el triángulo APC  es isósceles

entonces

y volviendo a bc

Hallar los ángulos sabiendo que .

y de aquí

donde obtenemos

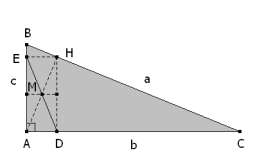
Sea M el punto medio de la altura por A. Se traza por M una recta DE cuya punto medio es M y está limitada por los catetos, se pide el valor de los ángulos en E y D en función de los del triángulo.

figura 3

A=90º  nos lleva a que ADHE sea un rectángulo. Que M  sea el punto medio de AH  nos lleva a que

y en consecuencia

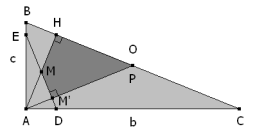
Sea M el punto medio de la altura por A. Se traza por M una recta DE cuya punto medio es M y está limitada por los catetos, se pide el valor de los ángulos en E y D en función de los del triángulo.

figura 4

Como MM’PH tiene dos ángulos opuestos de 90º, es inscriptible y

Pero ∠M’MA  es opuesto por el vértice a ∠HME  y en el cuadrilátero MHBE se cumple

y de aquí, en el triángulo BPA

y despejando

por lo tanto el triángulo BPA  es isósceles y así

y en el triángulo APC

que nos lleva a

por lo tanto el triángulo APC  es isósceles y así

y resumiendo

por lo tanto

¡¡ P y O coinciden !!