Problema 434
Siga un triangle rectangle en A, d’hipotenusa a, catets b, c, semiperímetre p i àrea S.
1.- Calculeu els catets en funció de la hipotenusa i l’àrea.
2.- Demostreu geomètricament que si els angles són de 15º i 75º, el producte dels catets és equivalent al quadrat de la meitat de la hipotenusa.
3.- Determineu els angles sabent que 
.
4.- Siga M el punt mig de l’altura per A. Es tracen una recta DE el punt mig de la qual és M, i està limitada pels catets. Es demana el valor dels angles en E i D en funció dels del triangle.
5.- Traçada la perpendicular per A a la recta DE, determineu la distància OP essent P el punt d’intersecció de dita perpendicular amb la hipotenusa i O el punt mig de la hipotenusa.
Solució:
1.-
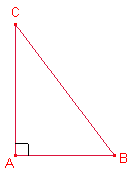Siga el
triangle rectangle 
, 
, 
.
L’àrea del triangle rectangle és 
.
Aplicant el teorema de Pitàgores: 
(1)
.
(2)
Considerem el sistema format per les expressions (1), (2)
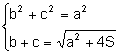. Resolent el sistema en les incògnites b, c:
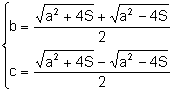
2.-
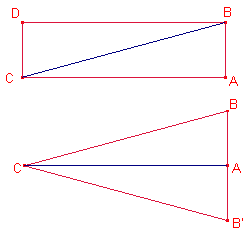
El producte bc és l’àrea del rectangle de costats b, c
Considerem el triangle rectangle , . 
.
Construïm el rectangle CABD. La diagonal del rectangle a.
L’àrea del rectangle és bc.
Siga B’ el punt simètric de B respecte de A.
El triangle 
té la mateixa àrea que
el rectangle CABD.
, 
.
L’àrea del triangle és 
.
Aleshores, 
, per tant, 
.
3.-
Siga
Aplicant el teorema de Pitàgores:
.
, aleshores, el triangle rectangle és isòsceles, per tant, 
.
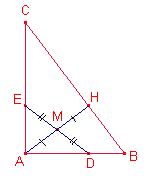
4.-
Siga M el punt mig de l’altura 
. Es tracen una recta DE el punt mig de la qual és M, i està
limitada pels catets.
Siga 
.
Els triangles , 
són semblants.
.
Per hipòtesi 
, 
.
Els triangles 
són semblants.
Aleshores, els segmentes 
són paral·lels.
Aleshores, ADHE és un rectangle. Per tant els triangles 
, 
són iguals.
Aleshores, 
, 
.
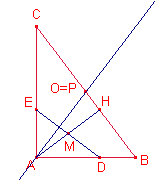5.-
La mitjana sobre la hipotenusa d’un triangle rectangle mesura la meitat de la hipotenusa. Siga O el punt mig de la hipotenusa.
Aleshores, 
. Per tant, 
Siga 
perpendicular a 
, aleshores, 
,
Aleshores, 
.
Per tant, la distància de P a O és nul·la.