Problema 434

Sea un triángulo rectángulo en A, de hipotenusa a, catetos b y c, semiperímetro p y área S.

·  Calcular los catetos en función de la hipotenusa y el área.

·  Demostrar geométricamente que si los ángulos agudos son de 15º y 75º, el producto de los catetos es equivalente al cuadrado de la mitad de la hipotenusa.

·  Hallar los ángulos sabiendo que .

·  Sea M el punto medio de la altura por A. Se traza por M una recta DE cuyo punto medio es M, y está limitada por los catetos. Se pide el valor de los ángulos en E y D en función de los del triángulo.

·  Trazada la perpendicular por A a esta recta DE, determinar la distancia OP siendo P el punto de intersección de dicha perpendicular con la hipotenusa y O el punto medio de la hipotenusa.

Propuesto por José María Pedret. Ingeniero Naval. (Esplugas de Llobregat, Barcelona)

Solución de Ricard Peiró:

1.-

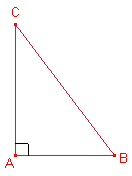Sea el triángulo rectángulo , , .

El área del triángulo rectángulo es .

Aplicando el teorema de Pitágoras:         (1)

.

                                                        (2)

Consideremos el sistema formado por las expresiones (1), (2)

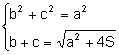. Resolviendo el sistema en las incógnitas b, c:

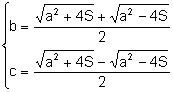
2.-

El producto bc es el área del rectángulo de lados b, c

Consideremos el triángulo rectángulo , . .

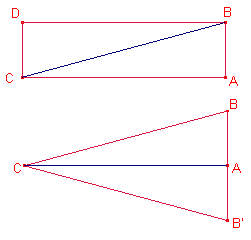
Construimos el rectángulo CABD. La diagonal del rectángulo a.

El área del rectángulo es bc.

Sea B’ el punto simétrico de B respecto de A.

El triángulo  té la misma área que el rectángulo CABD.

, .

El área del triángulo  es .

Entonces, , por tanto, .

3.-

Sea

Aplicando el teorema de Pitágoras:

.

, entonces, el triángulo rectángulo es isósceles, por tanto, .

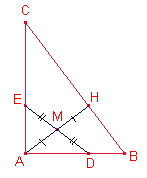
4.-

Sea M el punto medio de la altura . Se traza una recta DE el punto medio que es M, y está limitada por los catetos

Sea .

Los triángulos ,  son semejantes.

.

Por hipótesis , .

Los triángulos  son semejantes.

Entonces, los segmentos  son paralelos.

Entonces, ADHE es un rectángulo. Por tanto los triángulos ,  son iguales.

Entonces, , .

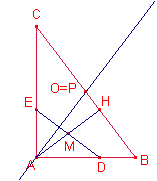5.-

La mediana sobre la hipotenusa de un triángulo rectángulo mide la mitad de la hipotenusa. Sea O el punto medio de la hipotenusa.

Entonces, . Por tanto,

Sea  perpendicular a , entonces, ,

Entonces, .

Por tanto, la distancia de P a O es nula.