Para el aula

Propuesto por José María Pedret. Ingeniero Naval. (Esplugas de Llobregat, Barcelona).

Problema 434.- Sea un triángulo rectángulo en A, de hipotenusa a, catetos b y c, semiperímetro p y área S.

1. Calcular los catetos en función de la hipotenusa y el área.

2. Demostrar geométricamente que si los ángulos agudos son de 15º y 75º, el producto de los catetos es equivalente al cuadrado de la mitad de la hipotenusa.

3. Hallar los ángulos sabiendo que .

4. Sea M el punto medio de la altura por A. Se traza por M una recta DE cuyo punto medio es M, y está limitada por los catetos. Se pide el valor de los ángulos en E y D en función de los del triángulo.

5. Trazada la perpendicular por A a esta recta DE, determinar la distancia OP siendo P el punto de intersección de dicha perpendicular con la hipotenusa y O el punto medio de la hipotenusa.

Pedret, J. M. (2007): Comunicación personal.

Solución

1.- Se tienen las expresiones

bc=2S

b²+c²=a²

Sumando y restando el doble de la primera a la segunda se tienen

(b±c)²= a²±4S

que permiten expresar los catetos en función de la hipotenusa y del área:

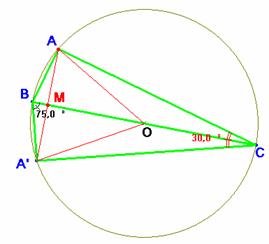 2.- Tomamos el simétrico del triángulo ABC respecto de la hipotenusa. Sea R el radio de su circunferencia circunscrita (que también lo es de ACA’). Como C = 30º, el ángulo central es el doble, siendo por tanto equilátero el triángulo OAA’, de donde R=AA’=a/2.

El área del cuadrilátero ABA’C es el doble del área del triángulo ABC y también la suma de las áreas de los triángulos isósceles ACA’ y ABA’. Se tendrá:

2bc =AA’·CM + AA’·BM=AA’·BC= 2·R²

o bien,  4·bc = a² como se pretendía demostrar.

3.-  En un triángulo rectángulo se verifica sen A + sen B + sen C =2p/a, pero sen A=1 y entonces la relación del problema se expresa como       sen B + sen C = .

Elevando al cuadrado y teniendo en cuenta que B y C son complementarios se obtiene

sen B ·sen C = 1/2.

Las soluciones de la ecuación           x² -x +1/2 = 0         son    sen B y sen C. Resolviendo sale sen B = sen C =/2.  El triángulo rectángulo es isósceles: los ángulos agudos miden 45º cada uno.

4.-  AM es una mediana del triángulo ADE. Al ser rectángulo es el radio de su circunferencia circunscrita. Como M es el punto medio de la altura AN, también N está en esta circunferencia, y áng (END) = áng (EAD) = 90º.

A y N son puntos diametralmente opuestos, por tanto, el cuadrilátero EADN es un rectángulo (una simetría central transforma EAD en DNE).

El ángulo AED es igual al ángulo AND y éste igual a b =ABC por tener sus lados perpendiculares.

Como consecuencia de lo anterior el ángulo en D es igual a g=ACB, quedando la situación como se muestra en el dibujo. Son semejantes ABC y AED.

5.-  El ángulo EAP = g (por la perpendicularidad de AP y ED), por ello PAD= b. De esto se deduce finalmente que son isósceles los triángulos CPA y APB: CP=AP=PB.

P es el punto medio de la hipotenusa, coincide con O. La distancia entre ambos es cero.