Problema 434. (Propuesto por J. M. Pedret, Ingeniero Naval. Esplugas de Llobregat, Barcelona).

Sea un triángulo rectángulo en A, de hipotenusa a, catetos b y c , semiperímetro p y área S.

1.- Calcular los catetos en función de la hipotenusa y el área.

2.- Demostrar geométricamente que si los ángulos agudos son de 15º y 75º, el producto de los catetos es equivalente al cuadrado de la mitad de la hipotenusa.

3.- Hallar los ángulos sabiendo que .

4.- Sea M el punto medio de la altura por A. Se traza por M una recta DE cuyo punto medio es M, y está limitada por los catetos. Se pide el valor de los ángulos en E y D en función de los del triángulo.

Resolución: (Vicente Vicario García, Huelva)

1.- Calcular los catetos en función de la hipotenusa y el área.

Plantearemos trivialmente el siguiente sistema de ecuaciones

                                    

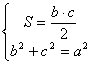
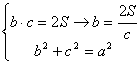
y efectuando la sustitución indicada llegamos a la siguiente ecuación bicuadrada

                                    

que se resuelve efectuando el cambio de incógnita , quedando entonces

                                              

cuyas soluciones  y  son la siguientes

                                   >0    si

            Deshaciendo el cambio, obtenemos el valor de los catetos en función de la hipotenusa y el área del triángulo:

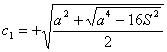                            y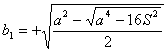   

y la otra solución simétrica

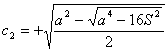                            y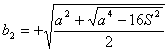   

2.- Demostrar geométricamente que si los ángulos agudos son de 15º y 75º, el producto de los catetos es equivalente al cuadrado de la mitad de la hipotenusa.

Observemos que es equivalente a . Por tanto, desde el punto de vista geométrico es suficiente con demostrar que el área de uno de estos triángulos rectángulos es la octava parte del área del cuadrado que tiene como lado su hipotenusa. Para la demostración geométrica, consideremos un cuadrado de vértices consecutivos ABCD y construyamos hacia el interior cuatro triángulos isósceles que tengan como ángulos de igual amplitud el valor 15º y como lado desigual, el lado del cuadrado considerado. Construimos así los puntos interiores E, F, G, H que debido a la simetría son claramente los vértices de un cuadrado y los cuatro triángulos isósceles AEB, BFC, CGD y DHA. Observemos, además, que cada uno de los triángulos BEF, CFG, DGH y AHE así formados son equiláteros puesto que tenemos que, de nuevo sin perder generalidad  y , etc.

            Por otra parte, dado un cuadrado, si construimos interiormente un triángulo equilátero teniendo uno de sus lados igual al del propio cuadrado, es fácil ver que el vértice (interior) del triángulo equilátero forma con los extremos del lado del cuadrado opuesto a su base, un triángulo isósceles de ángulo doble precisamente de valor 15º. Por tanto, considerando la construcción anterior relativa a los triángulos AEB, BFC, CGD y DHA, tenemos que los triángulos AEF y AEB son congruentes. Finalmente, basta observar que el área del triángulo AEF es claramente la mtad del área del cuadrado de vértices EFGH, con lo que el área de nuestros triángulos es obviamente la octava parte del área del cuadrado anterior.

3.- Hallar los ángulos sabiendo que .

            Con la notación habitual utilizada tenemos que  y . Puesto que . Entonces resolviendo esta ecuación trigonométrica tenemos que

                                  

y elevando al cuadrado y simplificando

                                                          

y efectuando una nueva elevación al cuadrado y simplificando

                                  

            Se puede comprobar que, efectivamente, esta solución es tal y no ha aparecido como solución extraña después de la doble elevación al cuadrado, ya que para este ángulo se tiene claramente que

                                  

4.- Sea M el punto medio de la altura por A. Se traza por M una recta DE cuyo punto medio es M, y está limitada por los catetos. Se pide el valor de los ángulos en E y D en función de los del triángulo.

            Sea A´ el pie de la altura sobre la hipotenusa. Supondremos, sin pérdida de generalidad que . Tracemos la circunferencia con centro en M y diámetro DE. Esta circunferencia claramente pasa por los puntos A y A´, ya que  y . Entonces AA´ y DE son diagonales del rectángulo inscrito AEA´D y en consecuencia A´E//AD con lo que  por ser  y  inscritos en la misma circunferencia y abarcar la misma cuerda. Entonces, de forma totalmente análoga, se deduce fácilmente que .

5.- Trazada la perpendicular por A a esta recta DE, determinar la distancia OP siendo P el punto de intersección de dicha perpendicular con la hipotenusa y O el punto medio de la hipotenusa.

            A partir de la semejanza de los triángulos BAA´ y ABC se obtiene fácilmente la relación

                                                          

            Además a partir del apartado anterior podemos afirmar que es cierta la relación .

            Si denotamos N el punto de corte de la perpendicular trazada desde A al segmento DE entonces se tiene . Además la longitud del segmento MA viene dada por, por lo que un simple tratamiento trigonométrico nos lleva (dada la definición de P) a la relación

                                  

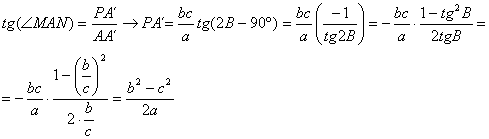
            Por otra parte, sabemos que O es el punto medio de la hipotenusa. Un cálculo sencillo nos lleva finalmente a

                                  

ya que , por lo que los puntos P  y O son siempre coincidentes, es decir, .