Problema 435.- (Propuesto por Alejandro Cipriano Coronel, UNASAM, Perú).

Se tiene un triángulo inscrito en una circunferencia de centro “O”. (“O” interior al triángulo), luego se trazan los segmentos desde el punto medio de los lados a la circunferencia perpendicularmente a los lados, llamados sagitas o flechas. Se pide calcular el área del triángulo inscrito en función de u, v y w, siendo u, v y w las medidas de las flechas o sagitas.

Resolución: (Vicente Vicario García, I.E.S. El SUR, Huelva)

Deduciremos una serie de relaciones previas relacionadas con los cosenos de los ángulos del triángulo dado.

Proposición: “Con la notación habitual para un triángulo sea A un ángulo del mismo, entonces cosA es una raíz real de la ecuación polinómica siguiente:

”.

Para la demostración consideremos las relaciones (teorema de los senos generalizado) y (relacionada con el incentro). Tenemos que utilizando las identidades trigonométricas del ángulo doble

Elevando al cuadrado y operando se tiene

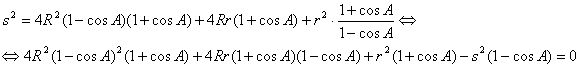
de donde, después de manipulaciones algebraicas, llegamos a la relación que queremos

Claramente esta relación se cumple también para y . De las relaciones de Cardano-Vieta entre las raíces y los coeficientes deducimos las relaciones

Utilizaremos la notación habitual en la geometría del triángulo. Sean R y r los radios de las circunferencias circunscrita e inscrita al triángulo. Al ser, por hipótesis, el triángulo de partida inscrito en una circunferencia de centro interior al mismo, es conocido que es acutángulo. Consideraremos u, v, w las longitudes de los segmentos medidos perpendicularmente desde el punto medio de cada uno de los lados a, b, c respectivamente, a los arcos menores de la circunferencia que circunscribe al triángulo. Sean D , E , F respectivamente, los puntos de corte de estos segmentos con los arcos de dicha circunferencia. En virtud del teorema del ángulo inscrito, y el hecho evidente de que , entonces se tiene que

y análogamente y . [1]

Por otra parte, el área del triángulo (utilizando el teorema de los senos generalizado) podemos escribirlo en la siguiente forma

2

y elevando al cuadrado

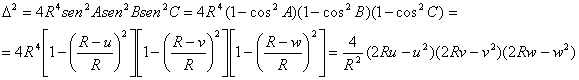con lo que, finalmente, tenemos que: [2]

Nos falta entonces expresar el radio R como función exclusiva de los valores u, v, w. Obtendremos que dicho valor se puede encontrar como solución de una ecuación polinómica de grado tres con coeficientes reales que son funciones racionales precisamente de u, v, w.

A partir de las expresiones [1] podemos obtener fácilmente las relaciones

y ,

Podemos plantear entonces

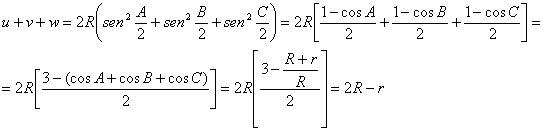
y de la clásica relación (cuya demostración, por no alargarnos demasiado, también se puede ver en mi artículo del extra 400 de esta revista), también tenemos

Entonces podemos resolver el sistema no lineal de ecuaciones

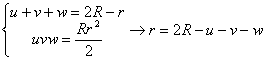
y llegamos a la relación

que tras simplificar nos lleva a la siguiente ecuación cúbica que permite, al resolverla, explicitar el valor de R como función exclusiva de u, v, w en términos de radicales

Al sustituir la raíz que corresponda a R en [2] en función de radicales, obtendremos la expresión pedida.

---oooOooo---

Nota: En virtud del teorema de Carnot, sabemos que en todo triángulo se cumple que la suma de las longitudes desde el circuncentro a sus lados es siempre . Por tanto, aplicando este teorema a nuestro problema y considerando los radios que contienen los puntos ya definidos anteriormente D, E, y F, tenemos claramente que