Problema 436

Siguen i dos triángulos tales que y , de lados a, b, c y a’, b’, c’, respectivamente.

Demostrar que . ¿Cuándo se alcanza la igualdad?.

Solución de Ricard Peiró:

Consideremos el triángulo , .

. La igualdad se alcanza cuando .

Supongamos .

.

. Dividiendo la desigualdad por :

.

, .

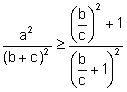Consideremos la función: , .

si

La función es decreciente en

Entonces, 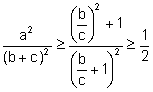, la igualdad se alcanza cuando .

Entonces, , la igualdad se alcanza cuando el triángulo es rectángulo y isósceles.

Por tanto, , la igualdad se alcanza cuando los dos triángulos son rectángulos y isósceles.