De investigación
Propuesto por Vicente Vicario García, I.E.S. “EL SUR”, Huelva
Problema 437
Sea dado un cuadrilátero convexo ABCD en el plano. Demostrar o refutar la existencia de un punto P en su interior de manera que las áreas de cada uno de los triángulos APB, BPC, CPD, DPA sean todas iguales entre sí.
Vicario, V. (2007): Comunicación personal.
Resuelto por JULIÁN SANTAMARÍA TOBAR profesor de Dibujo del IES
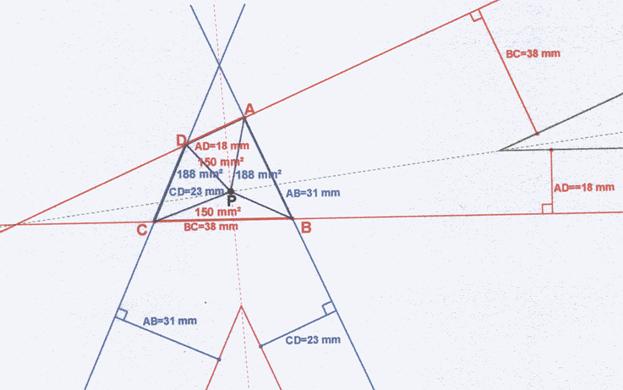
¿Habrá un punto P que al unirlo con los vértices delimite cuatro triángulos equivalentes?
El lugar geométrico de los puntos P que al unirlo por una parte con el segmento AB y por otra con el segmento opuesto CD formen dos triángulos equivalentes, es una recta. El área de los triángulos ABP y CDP es AB.H1/2 y CD.H2/2. La relación de distancias desde P a las rectas de los lados opuestos CD y AB será la relación de las alturas correspondientes a los triángulos equivalentes o sea: H1/H2 = CD/AB.
Si se repite el proceso con los otros lados opuestos BC y DA se obtendrá el lugar geométrico de los puntos que delimita con estos lados dos triángulos equivalentes.
Al hallar la intersección de los dos lugares geométricos se
habrán hallado dos parejas de triángulos equivalentes, pero los triángulos
adyacentes no tienen porqué ser iguales. En consecuencia no hay un punto P
que al unirlo con los vértices delimite cuatro triángulos equivalentes.
¿Habrá algún cuadrilátero en el que se cumpla la propiedad que consista en poder unir un punto P con los vértices y delimitar cuatro triángulos equivalentes en superficie?
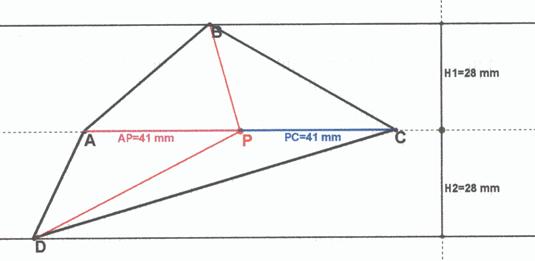
Uno se puede imaginar fácilmente dos triángulos con una base común (el segmento AC) y dos vértices el B y el D situados a distinto lado de la base y con la misma altura, o sea ABC equivalente a ACD. Si estos dos triángulos se dividen por las medianas correspondientes a la base común se habrá conseguido cuatro triángulos equivalentes cuya suma forman un cuadrilátero. Luego un cuadrilátero cuya diagonal lo divida en dos triángulos equivalentes, cumple la propiedad de tener un punto P tal que se pueda unir con los vértices y delimite cuatro triángulos equivalentes.
¿A parte del cuadrilátero cuya diagonal lo divide en dos triángulos equivalentes, habrá más cuadriláteros que cumplan la condición?
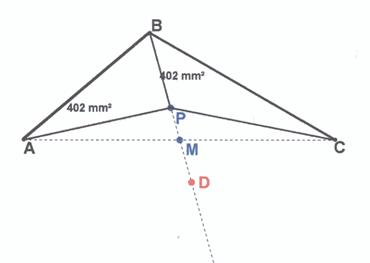
Vamos a considerar fijos tres vértices ABC del cuadrilátero que forman dos lados concurrentes. La recta donde estará el punto P para que se pueda unir con los vértices y delimite dos triángulos equivalentes es la mediana BM. La mediana BM es una recta que equidista de los vértices A y C por pasar por su punto medio M y al revés los vértices A y C equidistan de la mediana del tercer vértice B.
Fijado un punto P de la mediana BM Se puede repetir el proceso con el triángulo APC, y, se deduce que la recta donde podrá estar el punto D para que se pueda unir con los vértices y delimite triángulos equivalentes es la mediana PM que está sobre la recta BM. Es más, el vértice que falta D será el simétrico del vértice B respecto del punto P para que los cuatro triángulos que comparten el vértice P sean equivalentes. Luego el punto P está en una diagonal.
En definitiva el cuadrilátero, en el que una de sus
diagonales lo divide en dos triángulos equivalentes, es el único que cumple la
propiedad de tener un punto P tal que se pueda unir con los vértices y delimite
cuatro triángulos equivalentes.