De investigación. Propuesto por Vicente Vicario García, I.E.S. “EL SUR”, Huelva. Problema 437. Sea dado un cuadrilátero convexo ABCD en el plano. Demostrar o refutar la existencia de un punto P en su interior de manera que las áreas de cada uno de los triángulos APB , BPC , CPD , DPA sean todas iguales entre sí. Vicario, V. (2007): Comunicación personal Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (1 de febrero de 2008) |
|
ESTUDIO |
|
Sea un cuadrilátero ABCD cualquiera y supongamos que P existe.
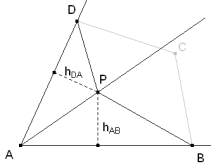
La igualdad de áreas, por ejemplo, de los triángulos PAB y PDA exige que
Lo que nos indica que el lugar de P es una recta que pasa por A y que las distancias de los puntos de la recta a las rectas AB y AD están en la proporción DA/AB. Análogamente, para el vértice B la recta pasa por B y la relación de distancias es AB/BC; para C la relación es BC/CD y para D es CD/DA.
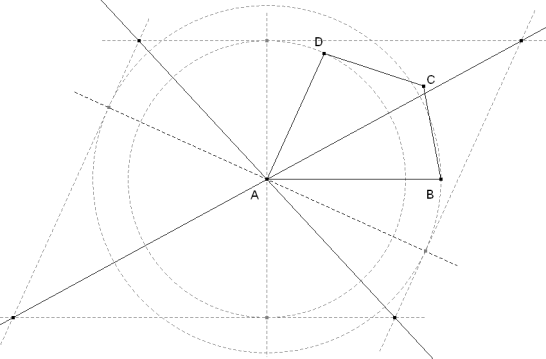
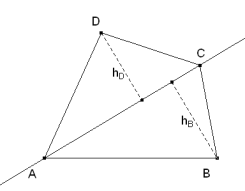
Detallamos la construcción para el vértice del lugar de P para el vértice A. Trazamos una paralela a AB a una distancia DA y una paralela a AD a una distancia AB, estos dos pares de paralelas se cortan en dos pares de puntos que proporcionan dos rectas (de trazo continuo en la figura 1).
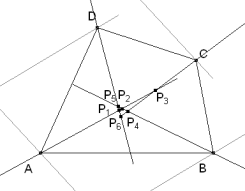
En general, obtenemos hasta ¡¡ seis !! puntos distintos en el interior del cuadrilátero. Para que este punto fuera solución, las cuatro rectas (cada una por un vértice) deberían ser concurrentes. Lo que significa, que fijados dos vértices, el cuarto dependería de la posición del tercero.
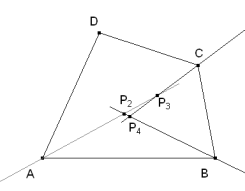
Tomemos, por ejemplo, las rectas por A y C (puntos que consideramos prefijados). Si nos fijamos en la recta por B vemos que obtendremos la solución si P2 y P4 coinciden; para ello basta que la recta por C coincida con la recta por A y entonces P3 puede ser cualquier punto de AC.
Si P está sobre AC, se cumple que el área del triángulo ABC es igual que la del triángulo CDA.
Condición que nos indica que después de fijar A y C si fijamos B, D debe estar sobre una paralela a AC a distancia hB Si además ABC (o CDA) debe quedar dividido en dos triángulos iguales P debe cumplir que
Es decir, P debe ser el punto medio de la diagonal AC. |
|
SOLUCIÓN |
|
|
Para que exista un punto interior P en un cuadrilátero ABCD cualquiera, de tal modo que las áreas de cada uno de los triángulos APB , BPC , CPD , DPA sean todas iguales entre sí, basta que un par de vértices opuestos equidiste de la diagonal que forma el otro par de vértices opuestos. Entonces, el punto P es el punto medio del otro par de vértices opuestos.
|