Problema 437

Siga donat un quadrilàter convex ABCD en el plànol. Demostreu o refuteu l’existència d’un punt P en el seu interior de manera que les àrees de cadascun dels triangles , , , siguen totes iguals.

Solució Ricard Peiró:

Considerem el quadrilàter ABCD convex amb les coordenades:

.

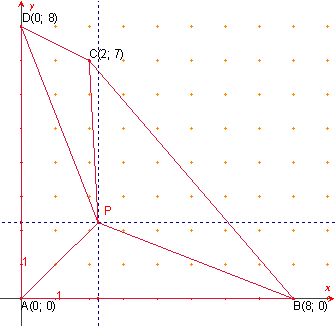
L’àrea del quadrilàter és 36.

L’àrea dels quatre triangles que cerquen és 9.

El vèrtex P del triangle està sobre la recta

El vèrtex P del triangle està sobre la recta .

Aleshores d’existir el punt P és la intersecció d’ambdues rectes, és a dir, el punt

Nota: aquest punt no té perquè estar dins del quadrilàter la qual cosa també refutaria l’enunciat.

Determinem l’àrea del triangle :

Determinem la recta que passa pels punts C, D:

.

.

.

.

.

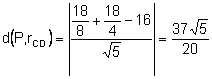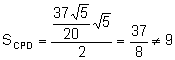Aleshores hi ha un quadrilàter convex que no acompleix la propietat.