Problema
437
Problema 437
Sea dado un cuadrilátero convexo ABCD en el plano. Demostrar o refutar la existencia de un punto P en su interior de manera que las áreas de cada uno de los triángulos APB , BPC , CPD , DPA sean todas iguales entre sí.
Solución
Ricard Peiró:
Considerem
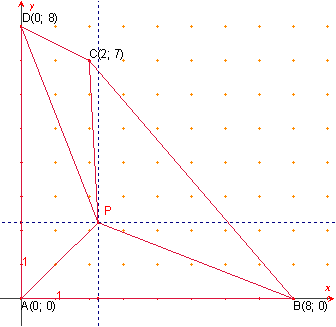
el cuadrilátero ABCD convexo con las coordenadas:
.
El
área del cuadrilátero es 36.
El
área de los cuatro triángulos que buscameos es 9.
El vértice
P del triángulo 
está sobre la recta 
El vértice
P del triángulo 
está sobre la recta 
.
Entonces
para existir el punto P tiene que ser la intersección de ambas rectas, es decir,
el punto 
Nota: este punto no tiene porque
estar dentro del cuadrilátero lo que también refutaría el enunciado.
Determinemos
el área del triángulo 
:
Determinemos
la recta que pasa por los puntos C, D:
.
.
.
.
.
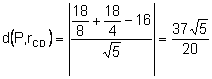Entonces
hay un cuadrilátero convexo que no cumple la propiedad.