Para el aula

Problema 438

Ejemplo 10

Demostrar que si la altura y la mediana desde el mismo vértice de un triángulo no isósceles son interiores al triángulo y forman ángulos iguales con sus lados cercanos, entonces es un triángulo rectángulo.

Gusev, V. Litvinenko, V y Mordovich, A. (1988): Solving problem in Geometry. Mir. Moscú.

Resuelto por JULIÁN SANTAMARÍA TOBAR profesor de Dibujo del IES La Serna de Fenlabrada

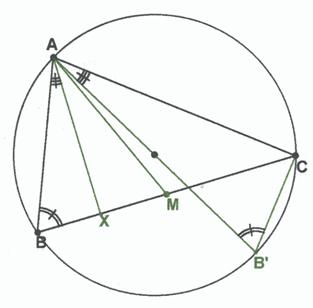
Supongamos fijos los vértices A y C en la circunferencia. El vértice B al desplazarse por la circunferencia, por abarcar la misma cuerda AC es constante. El triángulo rectángulo ABX (cuyo cateto AX es la altura del triángulo BAC) es semejante al triángulo diametral AB’C, Por lo tanto B’AC y BAX son iguales.

En consecuencia si el punto B se desliza por la circunferencia hasta que BC sea un diámetro, el pie de la mediana M coincidirá con el centro de la circunferencia, el ángulo A medirá 90º y la altura y la mediana del vértice A forman ángulos iguales con sus lados cercanos.