Problema 438

Ejemplo 10

Demostrar que si la altura y la mediana desde el mismo vértice de un triángulo no isósceles son interiores al triángulo y forman ángulos iguales con sus lados cercanos, entonces es un triángulo rectángulo.

Gusev, V. Litvinenko, V y Mordovich, A. (1988): Solving problem in Geometry. Mir. Moscú.

Solución de Ricard Peiró:

Si la altura de un triángulo está dentro del triángulo los otros ángulos distintos del que forma la altura son agudos.

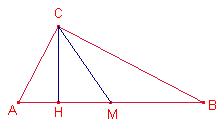Sea el triángulo , sea altura del triángulo tal que H pertenece al lado , sea la mediana del triángulo.

. .

Por hipótesis, .

.

.

.

Aplicando el teorema de los senos al triángulo :

.

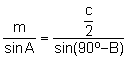Aplicando el teorema de los senos al triángulo :

.

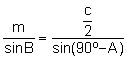Dividiendo ambas expresiones:

, .

.

Entonces , o bien, .

Entonces, , o bien, ,

Como el triángulo no es isósceles, , por tanto, . Por tanto el triángulo es rectángulo.