Problema 438.- Demostrar que si la altura y la mediana desde el mismo
vértice de un triángulo no isósceles son interiores al triángulo y forman
ángulos iguales con
sus lados adyacentes, entonces es un triángulo rectángulo.
(Gusev, V., Litvinenko, V. y Mordovich, A.
(1988). Solving problem in Geometry. Mir. Moscú).
Resolución: (Vicente Vicario García, I.E.S. El SUR, Huelva)
Utilizaremos la notación habitual en la geometría del triángulo. Para la resolución del problema necesitamos tres lemas que demostramos a continuación.
Lema 1: “Dado un triángulo ABC entonces la longitud de la mediana que parte del
vértice A es 
”.
Demostración: Sea D el punto de corte de la mediana que parte del vértice A con el lado BC. Aplicando el teorema de los cosenos al triángulo ABC tenemos que
y en virtud el teorema de los
cosenos aplicado al triángulo ABC,
podemos despejar 
en función de los lados del triángulo y llevar su valor a la
expresión anterior, quedando después de la simplificación oportuna
■
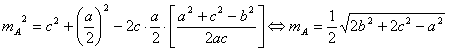Lema 2: “Dado un triángulo ABC entonces la longitud de la bisectriz interior que
parte del vértice A es 
”.
Demostración: Sea E el punto de corte de la bisectriz
interior que parte del vértice A con
el lado BC. Por el teorema de las
bisectrices, denotando 
, podemos plantear la relación
Aplicando el teorema de los cosenos al triángulo AEB y al triángulo ABC entonces
■
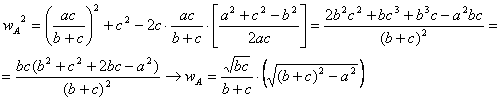Lema 3: “Dado un triángulo ABC 2si 
es la longitud de la
mediana que parte del vértice A y 
es la longitud de la
simediana (segmento simétrico del segmento mediana respecto de la bisectriz
interior 
) que parte del mismo
vértice, entonces se tiene la relación 
”.
Demostración: Sea F el punto de corte de la simediana que
parte del vértice A con el lado BC. Por definición de simediana se
tiene claramente que 
. Además, por el teorema de las bisectrices aplicado al
triángulo AFD (donde AE es bisectriz interior) tenemos la
relación
[1]
Por otra parte, a partir del contenido de la demostración del lema 2, es evidente que tenemos
Aplicando ahora el teorema de los cosenos al triángulo AED entonces
[2]
y aplicándolo al triángulo AEF entonces
[3]
Despejando 
en [2] y sustituyendo
en [3] tenemos que
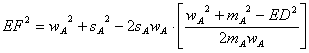[4]
Sustituyendo la relación [1] en [4], obtenemos la relación
y resolviendo esta ecuación de
segundo grado en la incógnita 
, obtenemos
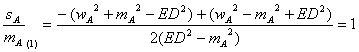
siendo éste el caso de triángulo isósceles, solución que no nos interesa, puesto que nuestro triángulo no lo es. La otra solución es
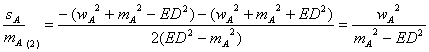
y aplicando los lemas 1 y 2 entonces
■
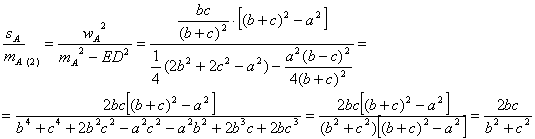Centrándonos
ahora en nuestro problema, se tiene que en las condiciones del mismo, la altura
que parte del vértice A, es decir, 
, es claramente tal que coincide con la simediana que parte
del mismo vértice. Por tanto, se ha de cumplir necesariamente, en virtud del
lema 3 anterior, la relación
y sustituyendo los valores
conocidos de , (utilizando la fórmula
de Herón†)
Elevando al cuadrado y simplificando tenemos
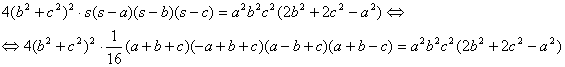
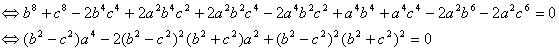
Puesto
que, por hipótesis 
, después de simplificar la ecuación anterior, llegamos a la
siguiente ecuación bicuadrada con dicriminante nulo
; 
.
Así
pues, resolviendo la ecuación tenemos fácilmente 
, y en virtud del recíproco al teorema de Pitágoras
concluimos que el triángulo ha de ser rectángulo en A, como requería el problema.
Nota: El teorema recíproco
también es cierto, es decir, en todo triángulo rectángulo la simediana que
parte del vértice del ángulo recto coincide con la altura que parte del mismo.
Por tanto, los ángulos que forma con los lados (catetos) adyacentes han de ser iguales.
La demostración es sencilla ya que por el teorema de Pitágoras . Además, se tiene la relación 
, que se obtiene fácilmente mediante relaciones de semejanza
o bien como aplicación conjunta de los conocidos teoremas de la altura y del
cateto
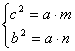
donde m y n son las proyecciones de los catetos c y b sobre la hipotenusa, respectivamente. Por otro lado, es claro que la mediana tiene como longitud
y por tanto
que obviamente se cumple por hipótesis.
