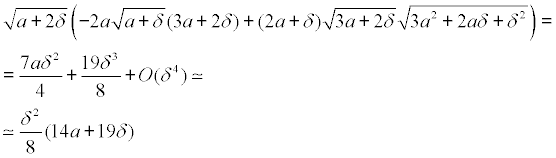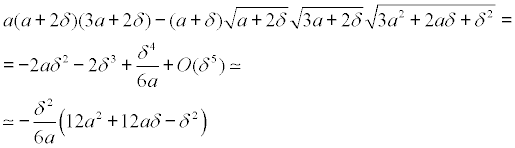De investigación. Propuesto por Juan Bosco Romero Márquez, profesor colaborador de la Universidad de Valladolid

Problema 439. Sea ABC un triángulo isósceles con la base variable c, y lados iguales a=b . Sean R, r, los radios del círculo circunscrito e inscrito, respectivamente; denotamos por hb, wb, mb, la altura, la bisectriz, la mediana del lado b, respectivamente. Calcular:

                   a) lim (R-2r)/(wb-hb) cuando c tiende a b,

                   b) lim (R-2r)/(mb-wb) cuando c tiende a b

                   c) lim (R-2r)/(mb-hb) cuando c tiende a b.

                    Nota. El límite se toma cuando los triángulos isósceles tienden a ser equiláteros.

Romero, JB. (2007): Comunicación personal.

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (15 de febrero de 2008)

SOLUCIÓN

Partimos de las expresiones de las distintas líneas del triángulo en función de los lados.

Podemos relacionar los lados del triángulo isósceles con δ tendiendo a cero y sustituir las raíces por sus infinitésimos equivalentes y nos queda

Lo que nos lleva a

Nota:

Quien esté interesado en los infinitésimos equivalente puede efectuar el desarrollo en serie de las expresiones que necesite, en función de δ y en el entorno de δ₀=0. En mi caso he usado para el primer denominador

,

para el segundo denominador

y para el tercer denominador
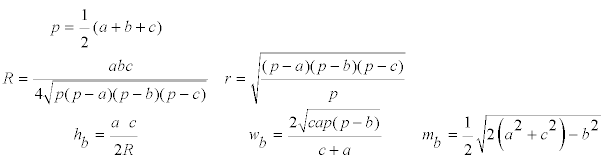
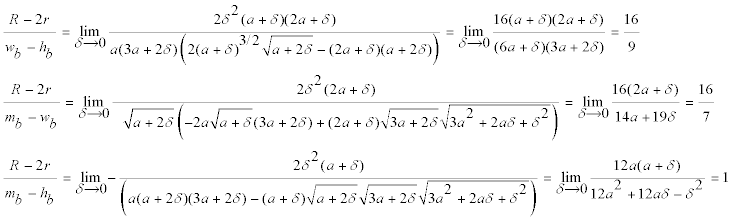
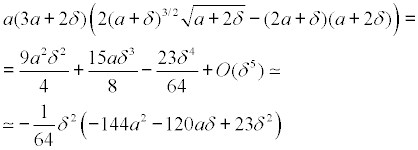