Problema 439

Sea el triángulo isósceles con la base variable c y los lados iguales .

Sean R, r los radios del círculo circunscrito y inscrito, respectivamente, denotamos por la altura, bisectriz y mediana del lado b, respectivamente. Calcular:

a) . b) . c) .

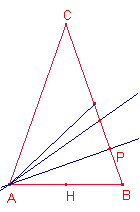Solución de Ricard Peiró:

Sea altura del triángulo.

Aplicando el teorema de Pitágoras al triángulo :

.

.

Entonces, , .

Aplicando la fórmula de la mediana de un triángulo:

.

La bisectriz referida a l’ángulo A es, .

Sea altura a los triángulos , son semejantes, aplicando el teorema de Tales:

.

a)

.

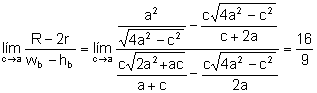Sin quitar generalidad al problema podemos suponer que .

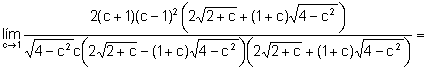
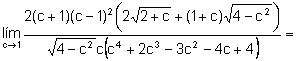
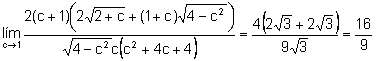
b)

.

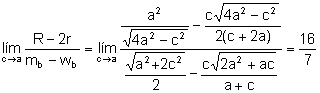Sin quitar generalidad al problema podemos suponer que .

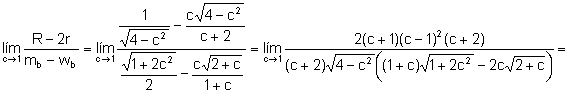
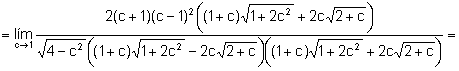
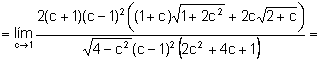
c)

.

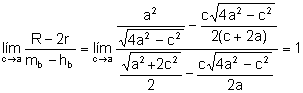Aplicando a) y b)

.
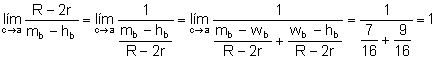