De investigación

Propuesto por Juan Bosco Romero Márquez, profesor colaborador de la Universidad de Valladolid

Problema 439.- Sea ABC un triángulo isósceles con la base variable c, y lados iguales  a=b . Sean R, r, los radios del círculo circunscrito e inscrito, respectivamente; denotamos por h_b, w_b, m_b, la altura, la bisectriz, la mediana del lado b, respectivamente.
          Calcular a)

b)

c) 

Nota. El límite se toma cuando los triángulos isósceles tienden a ser equiláteros.

Romero, JB. (2007): Comunicación personal.

Solución de Saturnino, Campo Ruiz, profesor del IES Fray Luis de León, de Salamanca.

Comenzaremos calculando las longitudes de R y de 2·r. El área de un triángulo cualquiera ABC es: [ABC]==1/2· (base)·(altura)=pr. Si tomamos como base el lado AB, podemos poner:

[ABC]===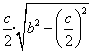= pr.

De aquí podemos obtener las expresiones de los dos radios. Además, por ser isósceles, a=b, 2p=2b+c. Se tienen ahora

R= , 2r ==

R - 2r== y

Cuando el lado c tiende a b, el triángulo se hace equilátero, entonces las medianas, bisectrices y alturas son iguales entre sí y su longitud es . La circunferencia inscrita tiene como diámetro el radio de la circunscrita, cualquiera de los tres límites adopta la forma indeterminada .

Se tendrá para cualquier par de estos segmentos desde el vértice B:

= =

a) En el dibujo BM es la mediana desde B, aunque el razonamiento que vamos a exponer ahora es válido también para la bisectriz. El triángulo BHM es rectángulo en H, por tanto la longitud del cateto MH puede obtenerse con el teorema de Pitágoras y también como diferencia (en valor absoluto) entre las longitudes de AM y AH.

Si BM=, por el teorema de la bisectriz, AM= y AH =. Así resulta =.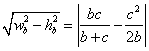

= .

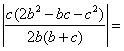
b) Aquí no nos sirve el argumento del triángulo rectángulo. Hemos de calcular la bisectriz y la mediana.

Para la mediana =. La bisectriz BM, observando el triángulo AMB (suponiendo que BM es la bisectriz) donde el ángulo en A es doble que en B, se obtiene, con el teorema de los senos, .

,

donde esta última expresión se ha obtenido calculando con mucha paciencia y teniendo en cuenta que la expresión debería ser nula cuando b y c fueran iguales.

De aquí, = .

c) Si BM=, razonando como en a), =

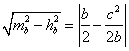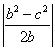= = y =1.