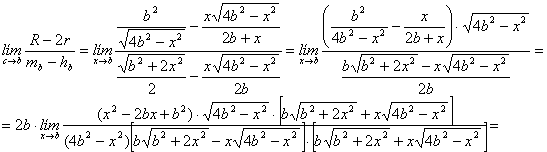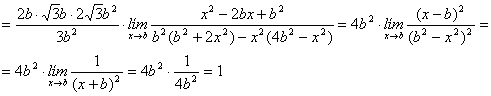Problema 439.- (Propuesto por J. B. Romero Márquez,
profesor colaborador de
Sea ABC un
triángulo isósceles con la base variable c,
y lados iguales 
, Sean R y r los radios de las circunferencias circunscrita
e inscrita, respectivamente. Denotamos por 
la altura, la
bisectriz interior y la mediana, relativas al lado b, respectivamente. Calcular:
(a) 
(b) 
(c) 
Nota: El límite se toma cuando los triángulos isósceles tienden a ser equiláteros.
Resolución: (Vicente Vicario García, I.E.S. El Sur, Huelva)
Nota: En este
problema calcularemos el límite del apartado (c) tal y como aparece, aunque
también proporcionamos el cálculo del límite que corresponde a sustituir en el
mismo el valor de 
por 
puesto que parece más acorde al enunciado del
problema y en analogía con los otros límites de los apartados (a) y (b).
Utilizaremos
la notación habitual en la geometría del triángulo. Comenzaremos asumiendo que son las longitudes de los lados iguales del triángulo
isósceles ABC y 
es la longitud del
lado desigual. Determinaremos expresiones para R, r, en función exclusivamente del lado b () constante y del lado variable. Sea D el punto medio del lado AB (de longitud c) variable.
A partir del teorema de los senos generalizado aplicado al triángulo ABC y del teorema de Pitágoras aplicado al triángulo CDB tenemos que
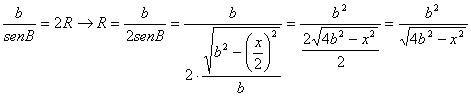
De la conocida
expresión 
para el área de un
triángulo, tenemos que
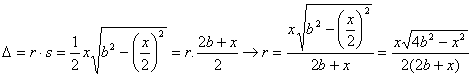
De la expresión
para el área determinamos la altura obteniéndose
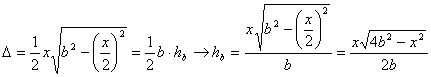
Para las expresiones relativas a 
y 
(por no extendernos demasiado)
pueden verse, por ejemplo, las demostraciones de los lemas 1 y 2 que propuse en
la resolución del problema 438 que aparecen en esta misma revista.
De esta forma, llegamos a las siguientes relaciones
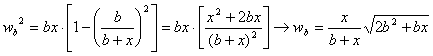
Pasemos a determinar los límites pedidos:
(a)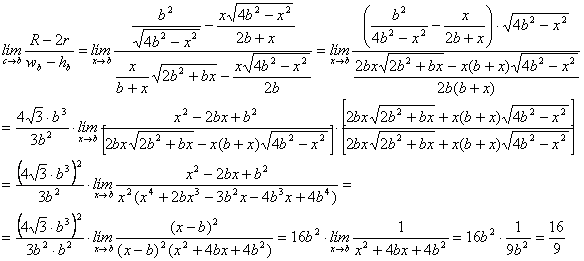 
El último límite de la anterior cadena de igualdades también se puede determinar, en lugar de con la factorización clásica de polinomios utilizando la regla de Ruffini, mediante la regla de L´Hôpital en la forma
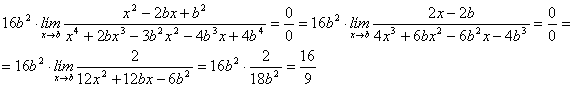
(b)
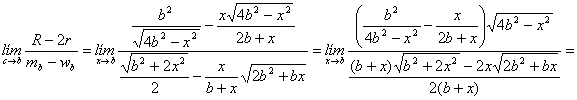
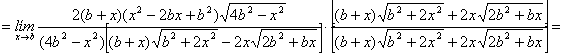
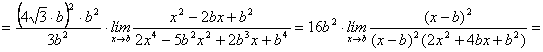
De nuevo, el último límite de la cadena de igualdades se puede también determinar con la regla de L´Hôpital
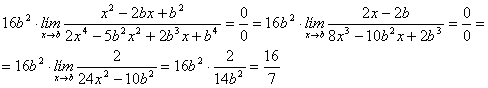
(c)
