Problema 440
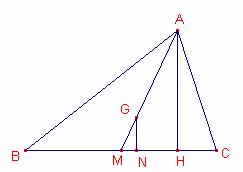
Sea G el baricentro de un triángulo ![]() . Siguen
. Siguen ![]() las distancias de G a los
lados a, b y c respectivamente. Sea r el radio de la circunferencia inscrita.
Probar que:
las distancias de G a los
lados a, b y c respectivamente. Sea r el radio de la circunferencia inscrita.
Probar que:
![]() . ¿Cuándo se alcanza la igualdad?.
. ¿Cuándo se alcanza la igualdad?.
Solución Ricard Peiró:
Sea ![]() la mediana del triángulo
la mediana del triángulo ![]() .
.
Sea ![]() altura del triángulo
altura del triángulo ![]() .
.
Sea ![]() .
.
Los triángulos ![]() son semejantes y la razón
es
son semejantes y la razón
es ![]() .
.
Entonces, ![]() .
.
![]() .
.
![]() .
.
![]() . Análogamente,
. Análogamente, ![]() ,
, ![]() .
.
![]() .
.
![]() .
.
Notemos que si ![]() , Aplicando la desigualdad entre la media aritmética y geométrica,
tenemos que,
, Aplicando la desigualdad entre la media aritmética y geométrica,
tenemos que, ![]() , la igualdad se alcanza cuando
, la igualdad se alcanza cuando ![]() .
.
Entonces:
![]() .
.
La igualdad s’e alcanza cuando ![]() , es decir, cuando el triángulo es equilátero.
, es decir, cuando el triángulo es equilátero.