De investigación

Propuesto por Vicente Vicario García, I.E.S. “EL SUR”, Huelva

Problema 440

Sea ABC un triángulo y G su baricentro. Denotamos por G_a , G_b, G_c las distancias desde G a los lados a, b, c del triángulo, respectivamente.

 Demostrar que G_a + G_b + G_c 3r, donde r es el radio de la circunferencia inscrita al triángulo, y caracterizar cuándo se da la igualdad.

Vicario, V. (2007) Comunicación personal.

Solución de Saturnino, Campo Ruiz, profesor del IES Fray Luis de León, de Salamanca.

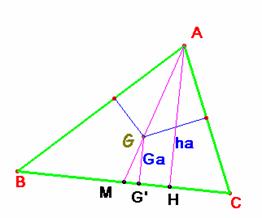
Por semejanza de los triángulos AMH y GMG’ se obtiene que G_a=·h_a. De otra parte si 2pr = 2[ABC] = a h_a, tenemos que G_a = y por tanto,

= =.

Los valores a, b, c son números reales positivos, por tanto también lo es cada sumando del tipo donde se agrupa una fracción (positiva) con su inversa. Bastará demostrar que cada uno de ellos es mayor o igual que 2. Demostrando esto hemos concluido.

En efecto llamando x =, tenemos x + 1/x - 2 = (x-1)²/x ≥ 0. El mínimo se alcanza cuando x= 1, o sea, a = b: corresponde al caso en el que el triángulo es equilátero y recíprocamente de forma trivial.