Para el aula
Propuesto por José María Pedret. Ingeniero Naval. (Esplugas de Llobregat, Barcelona)
Problema 441
Dado un triángulo cualquiera, dividirlo en dos partes de igual área.
(i) por medio de una recta paralela a uno de los lados.
(ii) por medio de una recta de dirección d determinada.
(iii) por medio de una recta perpendicular a uno de sus lados.
Pedret, J.M. (2008): Comunicación personal.
Resuelto por JULIÁN SANTAMARÍA TOBAR profesor de Dibujo del IES
i) Dividirlo en dos partes de igual área, por medio de una recta paralela a uno de los lados.
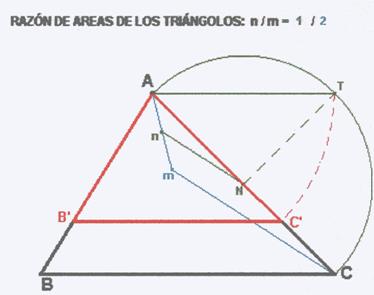
Los triángulo ABC y el AB’C’ son homotéticos luego la relación de los lados es la raíz cuadrada de la relación de las áreas.
ii) Dividirlo en dos partes de igual área, por medio de una recta de dirección r determinada.
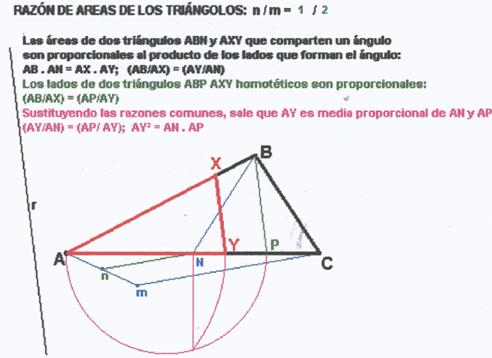
iii) Dividirlo en dos partes de igual área, por medio de una recta perpendicular a uno de sus lados.
Este ejercicio es un caso particular del anterior pero la resolución es la misma. Sin embargo he aplicado una construcción basada en homotecia que también es válida para el anterior.
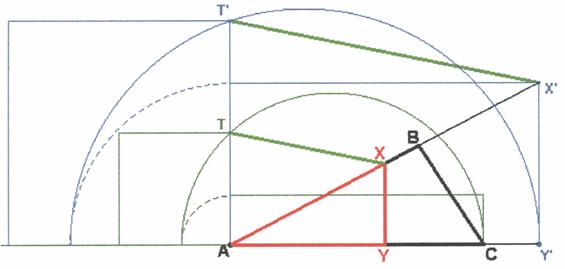
Sea el centro de homotecia del vértice A del triángulo dado ABC. A la izquierda se sitúan los cuadrados equivalentes y a la derecha los triángulos.
Se transforma triángulo ABC en el cuadrado de lado AT, ambos de la misma superficie. Este cuadrado tendrá el doble de superficie que el triángulo pedido.
Se toma un triángulo cualquiera AY’X’ homotético al pedido. Se transforma en un cuadrado de lado AT’ cuyo área sea el doble del triángulo.
T’X’ es paralelo a TX obteniendo así la recta XY perpendicular al lado AC pedida.