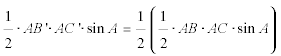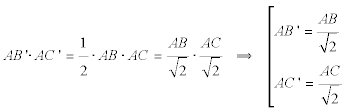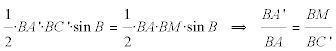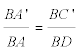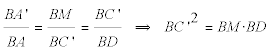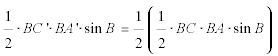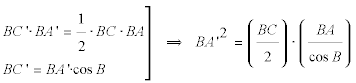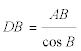Dado un triángulo cualquiera, dividirlo en dos partes de igual área por medio de una recta paralela a uno de los lados.

Si la sección es paralela a uno de los lados, por ejemplo a BC , se formarán dos triángulos homotéticos ABC∼AB’C’ con centro de homotecia en A.

Expresando que el área de AB’C’  tiene el área mitad de ABC  obtendremos la razón de homotecia

y ordenando convenientemente

de lo que deducimos que AC  es la diagonal de un cuadrado de lado AC’  (Análogo para AB ).

puede deplazar A

puede deplazar A

Si no está instaldo, descargar Cabri II Plus plug-in.

• Trazamos sobre AC  un cuadrado con su diagonal.

• El arco de centro A  que pasa por C determina sobre la diagonal AC”  de magnitud AC .

• Una paralela por C”  al lado del cuadrado determina C’  sobre AC.

• Una paralela por C’  a BC  nos proporciona la división pedida.

Dado un triángulo cualquiera, dividirlo en dos partes de igual área por medio de una recta de dirección d  determinada.

Suponemos que la paralela a la dirección d  que divide al triángulo ABC  en dos áreas iguales corta a AB  en A’ y a BC  en C’.

Comparamos el triángulo A’BC  con otro triángulo que tenga su misma área y conocido por nosotros; éste triángulo es AMB  donde AM  es la mediana por A de ABC.

Una paralela por A  a la dirección d  corta a BC  en D  y nos proporciona el triángulo ABD  homotético al triángulo A’BC’ que nos permite otro cálculo para la relación anterior

y combinando las dos ecuaciones

de donde obtenemos BC’  como la media geométrica de dos segmentos conocidos.

puede deplazar A y el vértice del vector d

puede deplazar A y el vértice del vector d

Si no está instaldo, descargar Cabri II Plus plug-in.

• Trazamos AM  la mediana por A.

• Trazamos por A  una paralela a d  que corta a BC  en D.

• Trazamos el semicírculo de diámetro MD.

• La tangente por B  al semicírculo tiene el contacto en el punto C”.

• Un arco con centro en B  y radio BC”  corta a BC  en C’.

• La paralela por C’  a d  corta a AB  en A’.

Dado un triángulo cualquiera, dividirlo en dos partes de igual área por medio de una recta perpendicular a uno de sus lados.

Suponemos la perpendicular al lado BC, que corta a BA en A’ y a BC en C‘.

Expresando que el área de A’BC’  es la mitad del área de ABC,  obtendremos la posición de A’.

ordenando convenientemente

Podemos hallar BA’  como la media geométrica de los dos segmentos puestos de manifiesto en la última ecuación

puede deplazar A

puede deplazar A

Si no está instaldo, descargar Cabri II Plus plug-in.

• Una perpendicular a AB  por A corta a BC  en D, 

• Un arco con centro en B y radio BD  corta a AB  en D’.

• Trazamos M  punto medio de BC.  Un arco con centro en B  y radio BM  corta a A B en M’.

• Trazamos el semicírculo de diámetro D’M’ .

• La tangente por B  al semicírculo tiene el contacto en el punto A”.

• Un arco de centro B  y radio BA”  corta a BA en A’.

• La perpendicular a BC  por A’  determina C’  sobre BC.