Problema 441

Donat un triangle qualsevol, dividiu-lo en dues parts d’igual àrea:

i) mitjançant una recta paral·lela a un dels costats.

ii) mitjançant una recta de direcció d determinada.

iii) mitjançant una recta perpendicular a un dels costats.

Solució de Ricard Peiró:

i)

Suposem resolt el problema:

Els triangles  i  són semblants, aleshores les àrees són proporcionals al quadrat de la raó dels triangles, per tant,

.

.

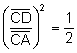És a dir  és la meitat de la diagonal d’un quadrat de costat .

Aquesta és la forma de construcció:

Dibuixar un quadrat de costat , exterior al trianlge.

Dibuixar el centre del quadrat O, .

Dibuixar la circumferència de centre C que passa per O, que talla el costat  en el punt D.

Dibuixar la recta paral·lela al costat  que passa per D que talla el costat  en el punt E.

Dibuixar el triangle .

Amb Cabri:

Figura barroso441a.fig

Applet created on 15/02/08 by Ricard Peiró with CabriJava

iii)

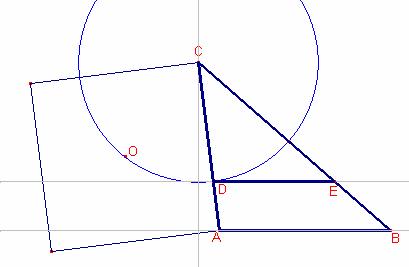
Si el triangle  és isòsceles, l’altura sobre els costat desigual divideix el triangle en dos triangles rectangles iguals.

Siga .

Suposem resolt el problema:

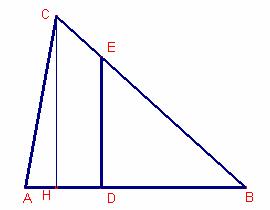
Siga  altura del triangle.

Siga , , .

Els triangles  i  són semblants, aplicant el teorema de Tales:

                                                     (1)

L’àrea del triangle  és la meitat de la del triangle , aleshores:

, aleshores,             (2)

Substituint l’expressió (2) en (1) i simplificant:

, aleshores,  és mitjana proporcional de .

Aquesta serà la forma de construcció.

Siga . Siga O el punt mig de .

Siga la circumferència de centre O que passa per B.

La recta CH talla la circumferència en el punt P .

Siga D tal que .

La recta perpendicular al costat  que passa per D talla el costat  en E.

Dibuixar el triangle .

Amb Cabri:

Figura barroso441c.fig

Applet created on 15/02/08 by Ricard Peiró with CabriJava

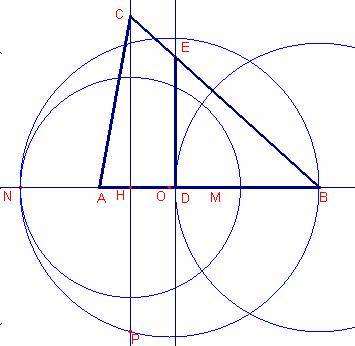
ii)

Si la Direcció és paral·lela a un costa aplicaríem i).

Construcció

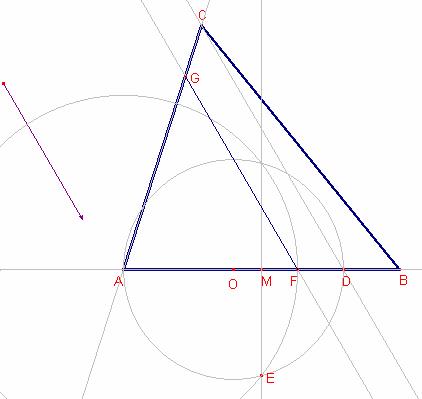
Dibuixem la recta que passa per C i és paral·lela a la direcció d. Aquesta recta talla la recta AB en el punt D.

Siga M el punt mig del costat .

Siga O el punt mig del segment .

Dibuixem la circumferència de centre O que passa pel punt A.

La recta mediatriu al costat  talla la circumferència en el punt E.

Siga F el punt del costat  tal que .

Dibuixem la recta paral·lela a la direcció d que passa pel punt F que talla el costat  en el punt G.

El triangle que cerquem és .

Justificació:

Siga . Siga . Siga .

Els triangles ,  són semblants, aleshores les àrees són proporcionals al quadrat de la raó dels costats:

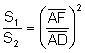                                  (3)

Els triangles ,  tenen la mateixa altura les àrees són proporcionals a les bases:

                                      (4)

Per construcció  és mitjana proporcional de  i .

Aplicant el teorema de Pitàgores al triangle rectangle :

           (5)

Multiplicant les expressions (3) (4)

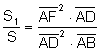                                            (6)

Substituint l’expressió (6) en (5):

.

Amb Cabri:

Figura barroso441b.fig

Applet created on 15/02/08 by Ricard Peiró with CabriJava