Problema 441

Dado un triángulo cualquiera, dividirlo en dos partes de igual área.

(i)    por medio de una recta paralela a uno de los lados.

(ii)   por medio de una recta de dirección d determinada.

(iii)  por medio de una recta perpendicular a uno de sus lados.

Pedret, J.M. (2008): Comunicación personal.

Solución de Ricard Peiró:

i)

Supongamos resuelto el problema:

Los triángulos  y  son semejantes, entonces las áreas son proporcionales al cuadrado de la razón de los triángulos, por tanto,

.

.

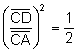Es decir  es la mitad de la diagonal de un cuadrado de lado .

Esta es la forma de construcción:

Dibujar un cuadrado de lado , exterior al triángulo.

Dibujar el centro del cuadrado O, .

Dibujar la circunferencia de centro C que pasa por O, que corta el lado  en el punto D.

Dibujar la recta paralela al lado  que pasa por D que corta el lado  en el punto E.

Dibujar el triángulo .

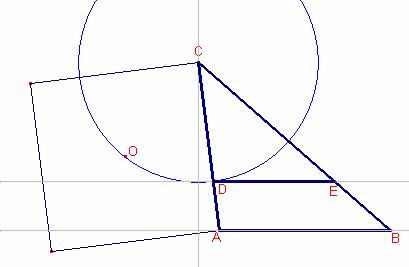
Con Cabri:

Figura barroso441a.fig

Applet created on 15/02/08 by Ricard Peiró with CabriJava

iii)

Si el triángulo  es isósceles, la altura sobre el lado desigual divide el triángulo en dos triángulos rectángulos iguales.

Sea .

Supongamos resuelto el problema:

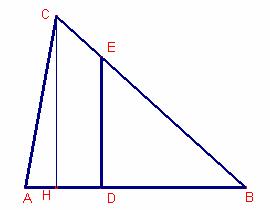
Sea  altura del triángulo.

Sea , , .

Los triángulos  y son semejantes, aplicando el teorema de Tales:

                                                     (1)

El área del triángulo  es la mitad de la del triángulo , entonces:

, entonces,             (2)

Substituyendo la expresión (2) en (1) y simplificando:

, entonces,  es media proporcional de .

Esta será la forma de construcción.

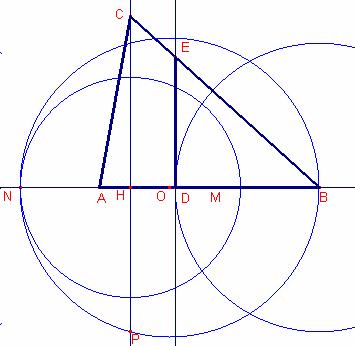
Sea . Sea O el punto medio de .

Sea la circunferencia de centro O que pasa por B.

La recta CH corta la circunferencia en el punto P .

Sea D tal que .

La recta perpendicular al lado  que pasa por D corta el lado  en E.

Dibujar el triángulo .

Con Cabri:

Figura barroso441c.fig

Applet created on 15/02/08 by Ricard Peiró with CabriJava

ii)

Si la dirección es paralela a un lado aplicaríamos i).

Construcción

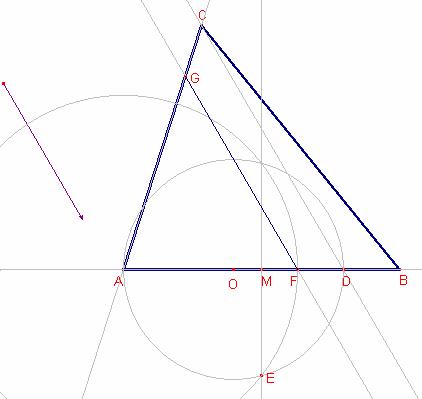
Dibujemos la recta que pasa por C y es paralela a la dirección d. Esta recta corta la recta AB en el punto D.

Sea M el punto medio del lado .

Sea O el punto medio del segmento .

Dibujemos la circunferencia de centro O que pasa por el punto A.

La recta mediatriz del lado  corta la circunferencia en el punto E.

Sea F el punto del lado  tal que .

Dibujemos la recta paralela a la dirección d que pasa por el punto F que corta el lado  en el punto G.

El triángulo que buscamos es .

Justificación:

Sea . Sea . Sea .

Los triángulos ,  son semejantes, entonces las áreas son proporcionales al cuadrado de la razón de los lados:

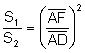                                  (3)

Los triángulos ,  tienen la misma altura las áreas son proporcionales a las bases:

                                      (4)

Por construcción  es media proporcional de  y .

Aplicando el teorema de Pitágoras al triángulo rectángulo :

           (5)

Multiplicando las expresiones (3) (4)

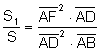                                            (6)

Substituyendo la expresión (6) en (5):

.

Con Cabri:

Figura barroso441b.fig

Applet created on 15/02/08 by Ricard Peiró with CabriJava