Para el aula

Propuesto por José María Pedret. Ingeniero Naval. (Esplugas de Llobregat, Barcelona)

Problema 441.- Dado un triángulo cualquiera, dividirlo en dos partes de igual área.

(i)  por medio de una recta paralela a uno de los lados.

(ii)  por medio de una recta de dirección d determinada.

(iii) por medio de una recta perpendicular a uno de sus lados.

Pedret, J.M. (2008): Comunicación personal.

Solución de Saturnino, Campo Ruiz, profesor del IES Fray Luis de León, de Salamanca.

i)

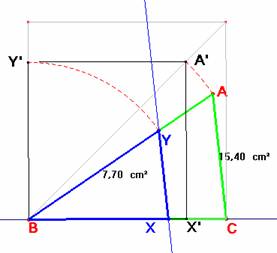
Con la paralela a un lado se forman dos triángulos semejantes, para que el área del menor sea la mitad del mayor, la razón de semejanza ha de ser . Esto es, BA=BY. Por tanto BA es la diagonal de un cuadrado cuyo lado es BY. Construimos un cuadrado cualquiera, por ejemplo de lado BC. Sobre su diagonal llevamos el lado BA=BA’. Se construye ahora el cuadrado BX’A’Y’ cuyo lado BY’=BY resuelve el problema.

ii) Trazamos por uno de los vértices, por ejemplo A, una paralela a la dirección dada. Se forma el triángulo BAA’ que es semejante al que buscamos. Este triángulo y el ABC tienen una altura común, por tanto para sus áreas podremos poner:

[BAA’] = [BAC]·.

Las áreas del triángulo solución BXY y su semejante a BAA’ son proporcionales al cuadrado de la razón de semejanza. Así pues

[BAA’] =[BXY]·.

Combinándolas se obtiene [BXY] = [BAC]·, y como su área ha de ser la mitad, entonces .

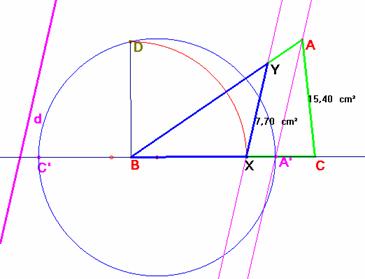
Se construye el segmento C’A’ cuya longitud es la suma de BA’ y BC/2 y se procede en la forma habitual como se muestra en la figura. El segmento BD es la media buscada que llevada sobre el lado BC determina X y resuelve el problema.

iii) Es un caso particular del anterior en que d es perpendicular al lado BC. Ahora BA’es la proyección de BA sobre BC. El resto es igual.