Problema 441.- (Propuesto por J. M. Pedret, Ingeniero Naval, Esplugas de Llobregat, Barcelona).
Dado un triángulo cualquiera ABC dividirlo en dos partes de igual área
(a) por medio de una recta paralela a uno de sus lados
(b) por medio de una recta de dirección determinada
(c) por medio de una recta perpendicular a uno de sus lados
Resolución: (Vicente Vicario García, I.E.S. El Sur, Huelva)
Mediante un sencillo argumento relativo a la continuidad de las funciones de una variable real, se demuestra que para cualquier dirección dada, existe una única recta que divide a un triángulo en dos partes de igual área.†
(a) Bisección del área por medio de una recta paralela a uno de sus lados.
A continuación daremos una construcción con regla y compás y después demostraremos tal construcción. Sea el triángulo ABC. Consideremos una base fija, por ejemplo, la base BC. Con centro en O punto medio del lado AC describimos una semicircunferencia exterior al triángulo de diámetro el lado AC. Determinamos el punto D de corte de la recta mediatriz del lado AC con dicha semicircunferencia. Haciendo centro en A y con radio AD describimos un arco hasta cortar en el punto E el lado AC, punto por el cual se traza la paralela a la base que divide el triángulo en dos partes de igual área. Denominaremos F al punto de corte de esta recta con el (otro) lado AB.
Demostración: Es
conocido que el ángulo 
determinado en la construcción anterior es un ángulo recto,
por ser inscrito y abarcar un diámetro. Por otra parte, en virtud del teorema
del cateto aplicado al triángulo ADC tenemos que
y además 
. Entonces
. [1]
Por otra parte, los triángulos ABC y AEF son semejantes, y en consecuencia
Designando 
al área del triángulo XYZ, entonces podemos plantear
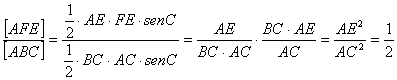(debido a [1])
demostrándose así la construcción proporcionada.
Nota: El mismo
método es válido para dividir el triángulo dado en n partes de igual área trazando paralelas a una base del triángulo
(consideramos BC como base). Se
dividiría el lado en n partes iguales
y se traza la semicircunferencia exterior al triángulo con centro en el punto
medio de un lado y diámetro dicho lado. Se levantan ahora perpendiculares por
las divisiones realizadas hasta cortar a la semicircunferencia en los puntos 
. Con centro en el vértice A y radios respectivos 
se describen arcos que
determinan sobre el lado AC los
puntos por los cuales han de trazarse las paralelas a la base BC y dividir el triángulo en n partes de igual área. Este método
sigue siendo válido para dividir de forma análoga el área de un triángulo en
partes proporcionales mediante paralelas a uno de sus lados, sin más que
utilizar el teorema de Thales para la división inicial del lado.
(b) Bisección del área por medio de una recta de dirección determinada.
Sea el triángulo ABC y consideremos una dirección 
determinada que no sea
paralela a uno de los lados del triángulo. Sabemos, por el teorema ya comentado
en el apartado (a) que existe una única recta con esa dirección que biseca el
triángulo en dos partes de igual área. De nuevo, daremos primero un
procedimiento de construcción con regla y compás para tal bisección y después
lo demostraremos.
Procedimiento: Sea el triángulo ABC. Sin pérdida de generalidad, podemos suponer que en la posición de bisección del área del triángulo, la recta, que denotamos por r, corta a los lados AC y AB del triángulo en los puntos P y Q respectivamente, con Q más cercano al vértice B que al C. Trazamos por el vértice A del triángulo una paralela a la dirección dada hasta cortar al lado CB en el punto D. Describimos después una semicircunferencia exterior al triángulo con centro el punto medio O del segmento CD. Por el punto medio M del lado CB trazamos una perpendicular hasta cortar la semicircunferencia en el punto E. Con centro en C y radio CE trazamos un arco que cortará en el punto Q al lado CB. Finalmente, la recta paralela a la dirección dada trazada por Q es la que divide al triángulo en dos partes de igual área, cortando al lado CA en el punto P.
Demostración:
Utilizaremos la notación para designar el área del triángulo XYZ. Es evidente la siguiente relación a partir de la construcción
efectuada
[1]
También es sabido que por la
construcción efectuada tenemos que 
. En virtud del teorema del cateto aplicado al triángulo CED tenemos
y como 
, debido a la construcción, entonces podemos plantear la
relación
[2]
Por otra parte, por la semejanza de los triángulos CPQ y CAD tenemos que
[3]
Sustituyendo [2] y [3] en [1] llegamos a
[4]
y como 
entonces
[5]
Finalmente, las áreas de los triángulos ABC y CAD están en la misma relación entre sí que la de sus bases, ya que tienen la misma altura referida a la misma base CB. Entonces tenemos que
[6]
y multiplicando las relaciones [5] y [6] se obtiene
demostrándose así la construcción dada.
(c) Bisección del área por medio de una recta perpendicular a uno de sus lados
De nuevo, por razones de continuidad, sabemos que existe una única recta bisectora perpendicular a un lado dado del triángulo. El mismo procedimiento del apartado (b) anterior es enteramente válido también en este caso. Siguiendo la misma notación, y sin perder la generalidad, basta con trazar por el vértice A la perpendicular al lado CB y continuar la misma construcción anterior.
Demostración: De nuevo debido a la
construcción tenemos que . Y aplicando el teorema del cateto al triángulo CDE se tiene que 
, pero como entonces
[1]
ya que . Por otra parte, de la semejanza de los triángulos
rectángulos CAD y CPQ tenemos la relación
[2]
Finalmente, utilizando las relaciones [1] y [2] entonces
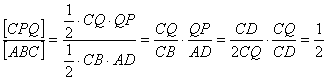
lo que demuestra la construcción.