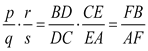Dadas dos fracciones, hallar su producto.

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (1 de marzo de 2008)

ESTUDIO

Partimos de la idea que este enunciado es para una revista especializada en TRIÁNGULOS.

Aprovechándonos de los triángulos enunciamos (y no demostramos) el TEOREMA DE MENELAO:

Si una recta corta a los distintos lados de un triángulo ABC respectivamente en los puntos D, E, F se cumple

.

En consecuencia podemos escribir

.

Supongamos que las fracciones dadas son

;

Basta tomar

y nos queda que la respuesta buscada es

Si enunciamos (y no demostramos) el TEOREMA DE CEVA:

Por medio de rectas, conectamos los vértices A, B, C de un triángulo cualquiera con un punto arbitrario O. Si cada recta corta al lado opuesto a su vértice en los puntos respectivos D, E, F entonces se cumple

.

Siguiendo pasos análogos al caso anterior, basta tomar

y nos queda que la respuesta es

Hemos obtenido dos métodos de solución que aplicamos a continuación en CABRI II Plus.

figura 1

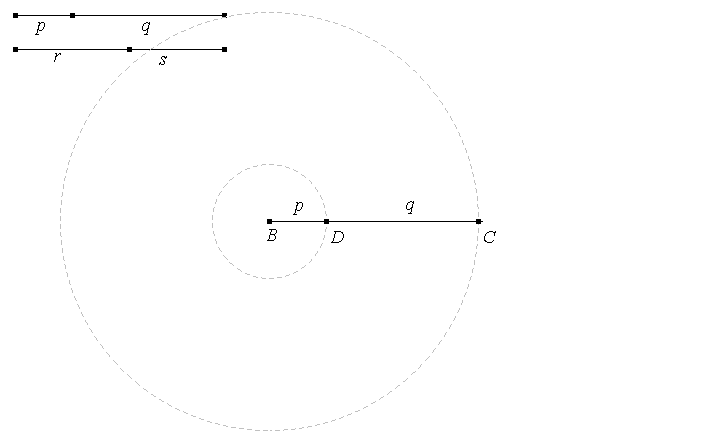
Dados p y q, trazamos una semi-recta cualquiera por un punto B.

Con centro en B y radio p, trazamos una circunferencia que corta a la semi-recta en D.

Con centro en B y radio p+q, trazamos una circunferencia que corta a la semi-recta en C.

figura 2

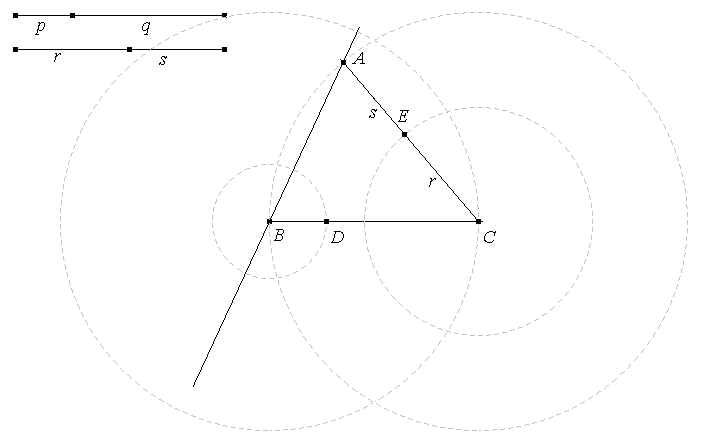
Dados r y s, trazamos una semi-recta cualquiera por el punto C.

Con centro en C y radio r, trazamos una circunferencia que corta a la semi-recta en E.

Con centro enC y radio r+s, trazamos una circunferencia que corta a la semi-recta en A.

Trazamos la recta AB.

Puede mover los objetos en rojo

figura 3 dinámica

(Primer método)

Una recta por D y E corta a la recta AB en F_m. AF_m y BF_m nos dan la solución buscada.

(Segundo método)

Las rectas AD y BE se cortan en un punto O. La recta CO corta a la recta AB en F_c. AF_c y F_cB nos dan la solución buscada.
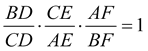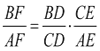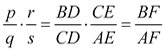
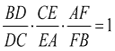