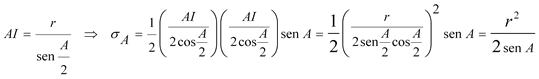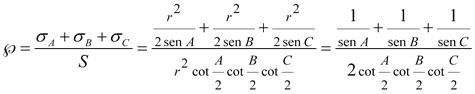De investigación. Propuesto por Vicente Vicario García, I.E.S. “EL SUR”, Huelva

Problema 444. Sea un triángulo ABC. Hallar la probabilidad de que escogido al azar un punto en su interior, dicho punto diste menos de alguno de los vértices del triángulo que del incentro I del mismo. Expresar el resultado exclusivamente en función de razones trigonométricas de los ángulos del triángulo.

Vicario, V. (2007): Comunicación personal

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (1 de marzo de 2008)

SOLUCIÓN

Aunque existen muchas discusiones filosóficas sobre el tema, entenderemos que la probabilidad pedida está vinculada proporcionalmente a las áreas de las figuras que intervienen en el enunciado.

figura 1

Si consideramos el universo com el área S del triángulo, la probabilidad del suceso pedido será según el conjunto de áreas sombreadas de la figura; donde las bases de los triángulos considerados son las mediatrices entre cada uno de los vértices y el incentro. En esas mediatrices, los puntos equidistan de alguno de los vértices y del incentro. Si el punto debe estar más próximo a un vértice que al incentro, estará dentro del área sombreada.

Si consideramos, por ejemplo el vértice A y llamamos σ_A al área sombreada en A

y como el área del triángulo se puede expresar en función de R y de las funciones trigonométricas de los ángulos (Trajan Lalesco, La géometrie du triangle 16.23, Éditions Jacques Gabay)

Nos queda la probabilidad pedida como

Resultado que con cualquier malabarismo trigonométrico puede presentar otro aspecto. Comprobaremos la bondad del resultado haciendo la comprobación dinámica con CABRI II Plus

Puede mover los elementos en rojo

figura 2 dinámica

Puede mover los elementos en rojo